K tomuto problému budeme přistupovat dvěma odlišnými způsoby. V prvním z nich
zformuluje soustavu rovnic, kde neznámými budou hledané váhy, a tuto soustavu
budeme řešit. V druhém případě (viz str. ![[*]](.//cross_ref_motif.gif) ) budeme
minimalizovat chybovou funkci sítě. K tomu použijeme buď gradientní metodu nebo
hledání minima položením prvních derivací minimalizované funkce rovných nule.
) budeme
minimalizovat chybovou funkci sítě. K tomu použijeme buď gradientní metodu nebo
hledání minima položením prvních derivací minimalizované funkce rovných nule.
V obou případech bude třeba vyřešit soustavu lineárních rovnic, která nemusí a ve většině případů nebude mít jednoznačné řešení. Budeme tedy hledat řešení, které je optimální ve smyslu nejlepších čtverců. Numerické metody nejmenších čtverců popíšeme v části 4.3.1
Nyní přistoupíme k prvnímu způsobu řešení. Chceme-li, aby síť pro vstupy
![]() z tréninkové množiny dávala odpovídající výstupy
z tréninkové množiny dávala odpovídající výstupy ![]() , musí
platit
, musí
platit
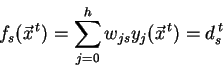 |
(4.17) |
Protože výstupy RBF jednotek už dokážeme spočítat, dostali jsme soustavu
lineárních rovnic s neznámými ![]() . Tu můžeme přepsat pomocí součinu matic jako
. Tu můžeme přepsat pomocí součinu matic jako
Matici ![]() výstupů RBF jednotek označme
výstupů RBF jednotek označme ![]() , matici
, matici ![]() vah
vah ![]() a matici
a matici
![]() požadovaných výstupů
požadovaných výstupů ![]() . Vztah (4.18) můžeme přepsat jako
. Vztah (4.18) můžeme přepsat jako
Obvykle máme více tréninkových vzorů než RBF jednotek a dostaneme tak přeurčenou soustavu rovnic. V tom případě hledáme takové řešení, jehož chyba je nejmenší. K tomu použijeme některou z metod nejmenších čtverců. Těmto metodám bude věnována část 4.3.1.
Nyní se podívejme na druhý přístup k hledání optimálních vah. Požadujeme, aby funkce
sítě co nejvíce odpovídala zadané tréninkové množině. To znamená, že chceme
minimalizovat funkci (2.12):
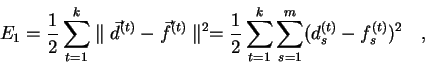
V 2.4.1 jsme uvedli problém regularizace, kdy na funkci sítě
klademe další požadavky, konkrétně chceme, aby příliš neoscilovala. Chybová
funkce je pak rozšířena o regularizační člen
První možnost je vyjádřit si derivace ![]() podle
podle ![]() a použít klasickou
gradientní metodu (viz 3.1). Tato metoda bývá obecně označována jako
LMS algoritmus (Least-Mean-Squares).
a použít klasickou
gradientní metodu (viz 3.1). Tato metoda bývá obecně označována jako
LMS algoritmus (Least-Mean-Squares).
Druhou možností je využití skutečnosti, že funkce nabývá lokálního extrému
právě tehdy, když jsou její první derivace rovny nule. První derivace chybové
funkce
![]() položíme rovny nule a pro
položíme rovny nule a pro
![]() a
a
![]() dostaneme
dostaneme
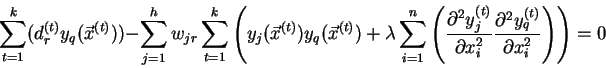 |
(4.21) |
| (4.22) |
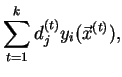 |
(4.23) | ||
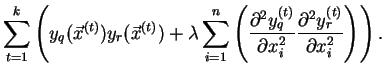 |
(4.24) |