Main Index Algebraic structures Structures with one operation Groups
  Subject Index
comment on the page

Cayley’s Group Theorem

Theorem (Cayley 1878). Every finite group of order is isomorphic to a group of permutations on elements.

Proof: We give an algorithm for a construction of such an isomorphism. If is the given group, let denote the group of permutations of the set with the standard composition of permutations.   

For define the map . This map is a biject due to the group axioms. It remains to prove that the map is an isomorphism, i.e. that . To see this, let . Then , or , that is   is a homomorphism. To prove that it is also injective it is sufficient to prove that the its kernel is trivial. If , where is the identical map, the due to the definition of we have with the identity of . On the other hand , i.e. showing that the kernel of is trivial.

The proof of Cayley’s theorem for finite groups depends on the fact that the group elements in a row of the Cayley table form a permutation of the original listing of the elements of the group. This observation gives another form of the previous proof is this: If is the standard representation of a permutation of an -element set, then denote by the permutation .  In this notation  . Note that each element corresponds to a permutation which consists of cycles which are of the same length and the length of each of the cycles in is just the order of .

For instance the Cayley table of the quaternion group is

If we substitute for the quaternions the numbers then the previous table takes the form

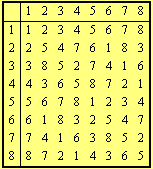
The rows as permutations of the basic set have the following cycle decompositions:

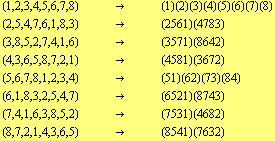
There is one further interesting fact contained in the above proof. The isomorphic image of is a subgroup of having order equal to the number of permuted elements and every permutation in the subgroup with the exception of the identity element has no fixed point. Such subgroups of the symmetrical group are called regular.  

Even if the proof of the theorem was constructive it is not always effective in the sense that the group is not “small” enough. For instance, let be the symmetry group of the equilateral triangle. Then is the symmetry group on 3 elements, that is, it has elements. In the above construction   is the symmetry group of a 6-elements set which has elements.

Note that every finite group can be embedded into the alternating group on elements which order is for .

Corollary. There exists only finitely many non-isomorphic groups of given order .

Corollary. The set of all non-isomorphic finite groups is countable.

Cayley’s theorem can be easily extended to infinite groups using formally the same idea:

Theorem . Every  group of cardinality is isomorphic to a group of  bijective transformations of a set of cardinality .

A permutation representation of a group G is a homomorphic representation of G as a group of permutations of a set. It is called faithful if the representation is injective.

A further generalization we get starting with a subgroup of finite index in a group (nor necessarily finite). Let be the set of right representatives of the right cosets with respect to then define .

Theorem. The above mapping is a homomorphic representation of the group . The kernel of this representation is a normal subgroup of , namely that which is maximal among those contained in .

Proof. That the mapping is homeomorphism is immediate. To prove the rest of the statement, let be its kernel. If then , i.e. for all . If we denote , then .  The intersection on the right hand side is clearly a normal subgroup of contained in . Since every normal subgroup of contained in   is contained in for each , . Thus and . In the opposite direction, if , then implying , i.e. .

Using Lagrange’s theorem we get:

Corollary. Each subgroup of finite index contains a normal subgroup of finite index, which is divisible by and divides .

References

Cite this web-page as: