Main Index Algebraic structures Structures with one operation Groups Special groups
  Subject Index
comment on the page

Quaternion Group

As the name indicates, the quaternion group is the multiplicative subgroup of Hamiltonian quaternions   generated the eight elements    and generating relations . Its Cayley table is

The powers of elements of the quaternion group are

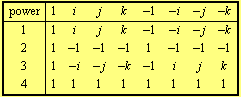
It is usually denoted by . It is one of the two non-Abelian groups of the five total finite groups of order 8. (The second one is the dihedral group ).

Lagrange’s theorem implies that every genuine subgroup of must be or order 2 or 4. There is a unique subgroup of order 2, namely , and three subgroups of order 4: , , and .  

Its center is . The factor group is isomorphic to the Klein four-group .  The quaternion group is the smallest non-Abelian group with all proper subgroups being Abelian. Moreover, the quaternion group the only group which all proper subgroups are Abelian and normal.  

The quaternion group is the smallest dicyclic group.

It is the smallest example of the so-called Hamiltonian groups, which are groups every subgroup of which is a normal group. Every Hamiltonian group contains a copy of .

It can be also given by the generating relations or , or as a group generated by two elements and , both of order 4 subject to the relations and . This gives the Cayley table

The isomorphism between these two forms is given by the rules: , , , .

The group can be also given in terms of permutations as a subgroup of the group . It is generated by permutations and . Then
,
,
,
and
.

Cite this web-page as: