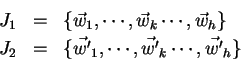


Next: Implementace
Up: Genetické algoritmy
Previous: Modifikace genetického učení
Obsah
Řešení problému vektorové kvantizace
V kapitole 4 jsme popsali tří fázovou metodu učení RBF sítí. Toto učení sestává
ze tří podúloh. Jednou z nich je řešení problému vektorové kvantizace.
Protože minimalizace chybové funkce (4.3) není triviální, metody
řešení vektorové kvantizace bývají založené na různých heuristikách a většinou
nabízejí pouze přibližné řešení.
Nabízí se tedy možnost, řešit problém vektorové kvantizace pomocí genetického
algoritmu.
Způsob kódování
Řešení problému vektorové kvantizace je tvořeno množinou 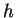 vektorů. Jedinec
bude tvořen zřetězením souřadnich těchto vektorů.
vektorů. Jedinec
bude tvořen zřetězením souřadnich těchto vektorů.
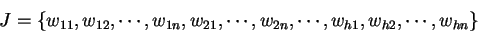 |
(5.6) |
Protože na pořadí vektorů nezáleží, můžeme použít kanonický algoritmus. V tomto
případě musí platit
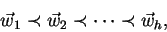 |
(5.7) |
kde 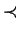 je uspořádání v lexikografickém pořadí.
je uspořádání v lexikografickém pořadí.
Počáteční populace
Počáteční populaci vytvoříme náhodně, v případě kanonického algoritmu vektory
před zakódováním setřídíme.
Účelová funkce 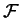
Stejně jako u učení neuronových sití 5.4 budeme hodnotit jedince
hodnotou chybové funkce
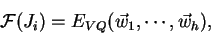 |
(5.8) |
kde 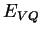 je chybovová funkce z vektorové kvantizace (4.3).
Čím menší ohodnocení, tím lepší řešení jedinec reprezentuje.
je chybovová funkce z vektorové kvantizace (4.3).
Čím menší ohodnocení, tím lepší řešení jedinec reprezentuje.
Selekce
Použijeme selekci popsanou v části 5.4.
Křížení
Použijeme jednobodové křížení. Křížením jedinců
získáme nové jedince
kde souřadnice 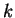 a
a 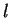 jsou zvoleny náhodně.
jsou zvoleny náhodně.
V případě kanonického algoritmu budeme bod křížení 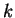 volit pouze na hranici bloků
odpovídajících jednotlivým vektorům
volit pouze na hranici bloků
odpovídajících jednotlivým vektorům
a výsledkem budou pouze jeden jedinec
nebo
Mutace
Náhodně vybereme jednu souřadnici a tu náhodně změníme. V případě kanonického
algoritmu náhodně vybere blok, který změníme náhodně s ohledem na zachování
uspořádání.
Výše uvedený algoritmus představuje alternativu metodám pro řešení vektorové
kvantizace uvedených v části 4.1. V případě, že přesně neznáme počet
reprezentantů, můžeme tyto genetické operátory upravit tak, aby pracovaly
s jedinci různé délky reprezentujícími řešení lišící se počtem reprezentantů. Do
ohodnocení takovýchto jedinců je pak třeba zahrnout penalizaci příliš dlouhých
jedinců.



Next: Implementace
Up: Genetické algoritmy
Previous: Modifikace genetického učení
Obsah
Petra Kudova
2001-04-19
![]() vektorů. Jedinec
bude tvořen zřetězením souřadnich těchto vektorů.
vektorů. Jedinec
bude tvořen zřetězením souřadnich těchto vektorů.
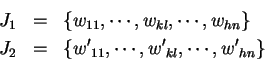
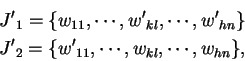
![]() volit pouze na hranici bloků
odpovídajících jednotlivým vektorům
volit pouze na hranici bloků
odpovídajících jednotlivým vektorům