Kanonický genetický algoritmus

Nyní se podívejme na možnost zrychlení předešlého algoritmu. Neruda popisuje v [7] tzv. kanonický genetický algoritmus pro učení RBF sítí. Klíčová myšlenka urychlení spočívá v omezení prohledáváného prostoru odstraněním redundancí.

Posloupnost všech parametrů sítě

$$P = \{ \mathcal{B}_1, \cdots, \mathcal{B}_h\}$$ (5.3)

$$\mathcal{B}_i = c_{i1}, \cdots, c_{in}, b_i, a^i_{11},\cdots, a^i_{nn} \quad i=1, \cdots, h$$

(viz kód sítě 5.2) nazveme parametrizací sítě. Na množině všech parametrizací zavedeme ekvivalenci tak, že dvě parametrizace prohlásíme za funkčně ekvivalentní právě tehdy, určují-li sítě realizující stejnou funkci. Prohledávání pak lze omezit na takový podprostor parametrického prostoru, který obsahuje právě jednoho zástupce každé třídy ekvivalence.

Nejjednodušším typem funkční ekvivalence je tzv. záměnná ekvivalence, t.j. permutace skrytých jednotek (permutace sčítanců sumy). V [9] je uveden důkaz věty, která říká, že každé dvě funkčně ekvivalentní RBF sítě s Gaussovou funkcí a metrikou indukovanou skalárním součinem jsou záměnně ekvivalentní.

Parametrizaci $P = \{ \mathcal{B}_1, \cdots, \mathcal{B}_h\}$ nazveme kanonickou, jestliže platí

$$\mathcal{B}_i \prec \mathcal{B}_{i+1},$$

kde $i=1, \cdots, h-1$ a $\prec$ je lexikografické uspořádání. Protože třída ekvivalence obsahuje právě takové parametrizace, které se vzájemně liší pouze permutací svých bloků, leží v každé třídě ekvivalence právě jedna kanonická reprezentace.

Nyní potřebujeme upravit náš genetický algoritmus tak, aby hledal řešení pouze mezi kanonickými reprezentacemi.

Kód jedince zůstává stejný jako v části 5.2, ale navíc platí, že $\mathcal{B}_i \prec \mathcal{B}_i+1$ pro $i=1, \cdots, h-1$. Proto musíme při vytváření počáteční populace generovat pouze jedince reprezentující kanonické parametrizace.

Dále musíme upravit genetické operátory, které vytvářejí nové jedince.

Křížením z 5.2 otce $I_1 = \{ \mathcal{B}_1, \cdots, \mathcal{B}_{h_1} \}$ a matky $I_2 = \{ \mathcal{D}_1, \cdots, \mathcal{D}_{h_2} \}$ vzniknou dva noví jedinci

$$\begin{eqnarray*} J_1 &= & \{ \mathcal{B}_1, \cdots, \mathcal{B}_s, \mathcal{D... ...thcal{D}_r, \mathcal{B}_{s+1}, \cdots, \mathcal{B}_{h_1-s+r}.\} \end{eqnarray*}$$

Protože platí $\mathcal{B}_s \prec \mathcal{B}_{s+1}$ a $\mathcal{D}_r \prec \mathcal{D}_{r+1}$ platí vždy alespoň jedna z nerovností

$$\begin{eqnarray*} \mathcal{B}_s & \prec & \mathcal{D}_{r+1} \\ \mathcal{D}_r & \prec & \mathcal{B}_{s+1}. \end{eqnarray*}$$

Výsledkem kanonického křížení bude pouze jeden jedinec, a to jedinec $J_1$ pokud $\mathcal{B}_s \prec \mathcal{D}_{r+1}$, jinak jedinec $J_2$.

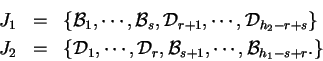
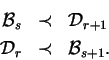
Mutace uvedená v části 5.2 vybere náhodně jeden blok $\mathcal{B}_i$ a jeho hodnotu náhodně změní. Kanonická mutace pracuje stejně, jen náhodná změna probíhá v mezích daných sousedními bloky $\mathcal{B}_{i-1}$ a $\mathcal{B}_{i+1}$. T.j. hodnotu bloku $\mathcal{B}_i$ nahradíme hodnotou $\mathcal{B}^{'}_i$, pro kterou platí $\mathcal{B}_{i-1} \prec \mathcal{B}^{'}_i \prec \mathcal{B}_{i+1}$.

Takto upravený genetický algoritmus pracuje nad $1/k!$ původního parametrického prostoru a dá se tedy očekávat, že řešení nalezne dříve.