Main Index Mathematical Analysis Special Functions
Subject Index
comment on the page

Gamma function

Gamma function typeset structure can be defined in many various ways. The following definition goes back to Euler (1729) and from that reason the defined function is also called Euler Gamma function or Euler function of the second kind .

Γ(z) = Underoverscript[∫, 0, arg3] e^(-t) t^(z - 1) d t = Underoverscript[∫, ... ;               Re(z) > 0(1)

The starting point of Euler’s definition was the identity  typeset structure which he used to extend the factorial function from the natural numbers to all real numbers typeset structure. Gauß introduced the notation typeset structure for typeset structure. Thus typeset structure for positive integers typeset structure. The name and notation typeset structure go back to A.-M. Legendre (1809)  (Cajori vol. 2, page 271). Legendre notation prevailed in France and later in the rest of world, despite the fact that Gauß “Pi” notation is more natural.

The Gamma function can be continued to the whole complex plane and it is there regular. As a function of complex variable has no zeros and  a pole of order one at each of the negative integers and at zero. The residue at typeset structure, is typeset structure.

This is graph of the Gamma function for real values of typeset structure:

[Graphics:HTMLFiles/GammaFunction_13.gif]

The minimum of typeset structure in interval typeset structure is typeset structure and it is attained at typeset structure.  The local minima of typeset structure converge to 0 for typeset structure. 

This is the graph of the absolute value of the Gamma function

[Graphics:HTMLFiles/GammaFunction_22.gif]

The behavior of typeset structure for large typeset structure is described in the so-called Stirling’s formula:  If  typeset structure is fixed then the equality

ln Γ(z + b) = (z + b - 1) ln z - z + 1/2 ln 2 π + O(| z |^(-1))(2)

holds uniformly in the range

| arg z | <= π - δ,         δ > 0,(3)

from which the point typeset structure and the poles of  typeset structure are cut off through small circles. The branches of  typeset structure and typeset structure should be taken  in such a way that their values are real at real positive typeset structure. This gives the following estimate:

If typeset structure and typeset structure are such that typeset structure then for typeset structure we have

| Γ(z) | = (2 π)^(1/2) | t |^(σ - 1/2) e^(π | t | /2) (1 + O(| t |^(-1))(4)

for typeset structure. The O-constant depends on typeset structure and typeset structure.

The first form of Stirling formula was found by de Moivre in the form typeset structure where typeset structure is a constant, the value of the constant was found by Stirling showing that typeset structure.  1

A simple form of Stirling formula can be proved easily

log n != Underoverscript[∑, k = 1, arg3] log k ~~ Underoverscript[∫, 1, arg3] log ... ] _ 1^n = n log n - n + 1 ~~ nlog n - n      =>    n ! ~~ n^n/e^n

Combined with the trapezoidal rule we get

n log n - n + 1 = [x log x - x] _ 1^n = Underoverscript[∫, 1, arg3] log x d x = Underove ... O(1) = log((n - 1) !) + (log n)/2 + O(1)     => n ! ~~ ϵ^c n^n n^(1/2)/e^n

for some constant typeset structure. More precise form of Stirling’s formula is

Underscript[lim, n -> ∞] n !/((2 π n)^(1/2) (n/e)^n) = 1.(5)

With the error estimates we have

n != (2 π n)^(1/2) (n/e)^n e^λ _ n          with       1/(12 n + 1) < λ _ n < 1/(12 n),(6)

or

n != (2 π n)^(1/2) (n/e)^n (1 + 1/(12 n) + 1/(288 n^2) - 139/(51840 n^3) - 571/(2488320 n^4) + 163879/(209018880 n^5) + ...),(7)

etc.

Euler found the following convergent product approximation for non-integral values typeset structure  

n ! ~~ [(2/1)^n 1/(n + 1)] · [(3/2)^n 2/(n + 2)] · [(4/3)^n 3/(n + 3)] ...(8)

This is the graph of the real part of the Gamma function

[Graphics:HTMLFiles/GammaFunction_52.gif]

This is the graph of the imaginary part of the Gamma function

[Graphics:HTMLFiles/GammaFunction_53.gif]

To compute values of  typeset structure go to .

Euler and Gauß defined the Gamma function originally also using the equivalent approach   .

Γ(z) = lim _ (n -> ∞) (n ! n^z)/(z(z + 1) ···(z + n)) = lim ... t;·(1 + z/n)) = z^(-1) Underoverscript[∏, n = 1, arg3] [(1 + 1/n)^z (1 + z/n)^(-1)] .(9)

Weierstrauß found the expression .

1/Γ(z) = z e^γz Underoverscript[∏, n = 1, arg3] [(1 + z/n) e^(-z/n)] ,(10)

where typeset structure is the Euler-Mascheroni constant.This is an entire function in the complex plane.

The graph of typeset structure for real values of the argument is:

[Graphics:HTMLFiles/GammaFunction_60.gif]

Integration per parts yields from (1) the important functional equation

Γ(z) = 1/z Underoverscript[∫, 0, arg3] e^(-t) t^z d t = 1/z Γ(1 + z),(11)

or in other words

Γ(z + 1) = z Γ(z) . (12)

Consequently, if typeset structure then

Γ(z + n) = z(z + 1) (z + 2) ···(z + n - 1) Γ(z) .(13)

For typeset structure, the important connection to the factorial function easily follows

Γ(n + 1) = n !       for      n ϵ N . (14)

Since

sin(πz) = πz Underoverscript[∏, n = 1, arg3] (1 - z^2/n^2) ,

Weierstrauß relation (10) implies

Γ(z) Γ(-z) = -π/(z sin(πz)) = -zΓ(-z) Γ(z)(15)

This gives the relations (the first of them is called the Euler's reflection formula)

Γ(z) Γ(1 - z) = π/(sin (πz))(16)
Γ(1/2 + z) Γ(1/2 - z) = π/(cos (πz))(17)
(Γ(n + z) Γ(n - z))/[(n - 1) !]^2 = πz/(sin (πz)) Underoverscript[∏, k = 1, arg3] (1 - z^2/k^2) ,           n ϵ N,(18)
(Γ(n + 1/2 + z) Γ(n + 1/2 - z))/[Γ(n + 1/2)]^2 = 1/(cos (πz)) Underoverscrip ... ] (1 - (4 z^2)/(2 k - 1)^2) ,           n ϵ N .(19)

Relation (16)  implies for typeset structure that

Γ(1/2) = 2 Underoverscript[∫, 0, arg3] e^(-v^2) d v = π^(1/2),(20)

and for typeset structure and typeset structure we get

Γ(1/3) Γ(2/3) = (2 π 3^(1/2))/3

Γ(1/4) Γ(3/4) = π 2^(1/2) .

Note that no simple expression is known for typeset structure,  typeset structure and typeset structure. However, it was proved that these numbers are transcendental ( the first one by Le Lionnais  [1] , p.46 in 1983 and two others by Chudnovsky [2] ,p. 308] in 1984 respectively).

Borwein and  Zucker  [3] showed how to reduce the evaluation of the gamma function at rational values by expressing gamma functions at rational values in terms of elliptic integrals. For instance

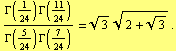
(Γ(1/24) Γ(11/24))/(Γ(5/24) Γ(7/24)) = 3^(1/2) (2 + 3^(1/2))^(1/2) .

We also have

FormBox[RowBox[{Γ(n/2) = ((n - 2) !! π^(1/2))/2^(n - 1)/2, , ,,    &nb ... p;  n !!    denotes the double factorial ), Cell[], Cell[], }]}], TraditionalForm]

Legendre discovered the following duplication formula

Γ(2 z) = 2^(2 z - 1) π^(-1/2) Γ(z) Γ(z + 1/2) ,(21)

which was by Gauß extended to Gauß-Legendre multiplication formula

Underoverscript[∏, k = 0, arg3] Γ(z + k/m) = (2 π)^(m - 1)/2 m^(1/2 - mz) Γ ... nbsp;    m = 2, 3, 4, ···       (22)

In the above mentioned  Gauß Pi notation the multiplication formula has the form

Π(z/m) Π((z - 1)/m) ···Π((z - m + 1)/m) = ((2 π)^m/(2 πm))^(1/2) m^(-z) Π(z) .

Since typeset structure for typeset structure, we can take the logarithm to get

ln(Γ(z)) = -γ - 1/z + Underoverscript[∑, n = 1, arg3] (z/n - ln(1 + z/n)) .

FormBox[RowBox[{Cell[Γ(z)], , belongs, , to, , class, , C^∞, , the, , derivative, , of, , the, , above, , formula, , gives}], TraditionalForm]

Γ^'(z)/Γ(z) = - γ - 1/z + Underoverscript[∑, n = 1, arg3] z/n(z + n) .

We also have

Γ^'(z)/Γ(z) = ln z - 1/(2 z) + O(1/(| z |^2))(23)

for typeset structure, typeset structure. The O-constant depends on typeset structure.

A natural question in what extend the functional equation  (12) determines the gamma function. The answer was given by the Bohr and Mollerup  [4] :  

There is a unique function typeset structure such that typeset structure is convex and typeset structure, and typeset structure.

The formula for the surface area of the typeset structure-dimensional sphere typeset structure is

2 (π^(n/2) r^(n - 1))/Γ(n/2) .

and its volume is

FormBox[RowBox[{RowBox[{(π^(n/2) r^n)/Γ(n/2 + 1), , ., Cell[]}], Cell[]}], TraditionalForm]

Notes

1 In the proof that typeset structure the Wallis formula is instrumental.

References

[1]  Le Lionnais, F. (1979). Les nombres remarquables. Paris: Hermann.

[2]  Chudnovsky, G. V. (1984). Contributions to the theory of transcendental numbers. Providence, RI: Amer. Math. Soc.

[3]  Borwein, J. M., & Zucker, I. J. (1992). Fast evaluation of the gamma function for small rational fractions using complete elliptic integrals of the first kind. IMA J. Numer. Anal., 12(4), 519-526.

[4]  Bohr, H., & Mollerup, J. (1922). Laerebog i matematisk analyse, vol. 3  Graenseprocesser. (Danish). Kopenhagen: J. Gjellerup.

Cite this web-page as:

Štefan Porubský: Gamma Function.

Page created  . Last modified .