Main Index Number Theory Continued fractions
  Subject Index
comment on the page

Basic definitions for continued fractions

A continued fraction is an expression of the form

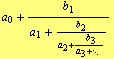a _ 0 + b _ 1/(a _ 1 + b _ 2/(a _ 2 + (   b _ 3)/(a _ 3 + _ ·.   )))(1)

where typeset structure, and typeset structure are either real or complex values called the terms of continued fraction (1). The number of terms can be either finite (typeset structure) or infinite (typeset structure). If typeset structure continued fraction (1) is called finite, otherwise infinite. The typeset structure’s are called partial denominators and typeset structure’s partial numerators.

Thought the notation used for a continued fraction in (1) is intuitive and lucid, it takes up a lot of space and is not easy to typeset. So several alternative notations were developed. For instance,  A.I. Pringsheim introduced the notation

a _ 0 + (b _ 1 |)/(| a _ 1) + (b _ 2 |)/(| a _ 2) + ... ,

while C.F.Gauß used

a _ 0 + Underscript[Overscript[Κ, ω], i = 1]    b _ i/a _ i ,

where K stands for the initial of German mane Kettenbrüche for continued fraction.

The rational value

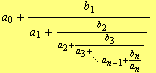a _ 0 + b _ 1/(a _ 1 + b _ 2/(a _ 2 + b _ 3/(a _ 3 + _ (·.    a _ (n - 1) + b _ n/a _ n))))(2)

or

a _ 0 + (b _ 1 |)/(| a _ 1) + (b _ 2 |)/(| a _ 2) + ... + (b _ n |)/(| a _ n)

or

a _ 0 + Underscript[Overscript[Κ, n], i = 1]    b _ i/a _ i ,

which we get by truncation of the original continued fraction  after the typeset structureth partial denominator typeset structure, typeset structure, is called the typeset structureth convergent of the given continued fraction.

The first four convergents are

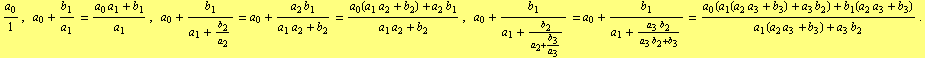a _ 0/1 ,    a _ 0 + b _ 1/a _ 1 = (a _ 0 a _ 1 + b _ 1)/a _ 1 ,    a _ 0 ... + b _ 3) + a _ 3 b _ 2) + b _ 1(a _ 2 a _ 3 + b _ 3))/(a _ 1(a _ 2 a _ 3 + b _ 3) + a _ 3 b _ 2) .(3)

Although a given convergent may naturally  be worked out “from the bottom” as it was done above, it is more practical to generate the sequence of convergents “from the top” . Let typeset structure, typeset structure denote the numerator and the denominator of the typeset structureth convergent. J.Wallis  [1] ,  [2]  and L.Euler  [3]  found that the values of typeset structure, and typeset structure can be determined recursively

P _ n = a _ n P _ (n - 1) + b _ n P _ (n - 2)(4)

Q _ n = a _ n Q _ (n - 1) + b _ n Q _ (n - 2)(5)

for typeset structure and initial conditions  typeset structure, typeset structure, typeset structure, typeset structure. It is sometimes useful to start with typeset structure, typeset structure, typeset structure, typeset structure, or with  typeset structure, typeset structure, typeset structure, typeset structure.

Recurrence relations (4) and (5) are called fundamental recurrence formulas and the fraction

P _ n/Q _ n ,    n = 0, 1, 2, ...(6)

is the typeset structureth convergent of (1).

For the sake of simplicity it is usually supposed that all typeset structure are non-vanishing.

We say that the continued fraction (1) converges or diverges (or oscillates) if the sequence typeset structure converges or diverges (or oscillates) for typeset structure. If the continued fraction (1) converges, that

lim _ (n -> ∞) P _ n/Q _ n = ξ,(7)

then typeset structure is assigned as the value of (1).

Theorem (  [4]  , Satz 1): Let every typeset structure, typeset structure, be non-vanishing.  It two of three equalities

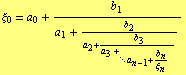ξ _ 0 = a _ 0 + b _ 1/(a _ 1 + b _ 2/(a _ 2 + (   b _ 3)/(a _ 3 (+ _ (·. a _ (n - 1) + b _ n/ξ _ n) ) _ )))(8)

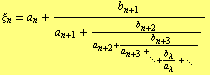ξ _ n = a _ n + b _ (n + 1)/(a _ (n + 1) + b _ (n + 2)/(a _ (n + 2) + (   b _ (n + 3))/(a _ (n + 3) (+ _ (·. + b _ λ/a _ λ (+ ) _ ·.) ) _ )))(9)

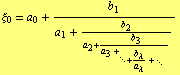ξ _ 0 = a _ 0 + b _ 1/(a _ 1 + b _ 2/(a _ 2 + (   b _ 3)/(a _ 3 (+ _ (·. + b _ λ/a _ λ (+ ) _ ·.) ) _ )))(10)

are valid, then also the third one is true, no matter whether the continued fractions  (9),  (10) are infinite or finite but ending with the same term.

Theorem: We have:

P _ n/Q _ n - P _ (n - 1)/Q _ (n - 1) = ((-1)^n b _ 1 b _ 2 ... b _ n)/(Q _ n Q _ (n - 1)),(11)

P _ (n + 1)/Q _ (n + 1) - P _ (n - 1)/Q _ (n - 1) = ((-1)^(n + 1) b _ 1 b _ 2 ... b _ n a _ (n + 1))/(Q _ (n + 1) Q _ (n - 1)) ,(12)

P _ n/Q _ n = b _ 0/Q _ 0 + b _ 1/Q _ 1 - (b _ 1 b _ 2)/(Q _ 1 Q _ 2) + (b _ 1 b _ 2 b _ 3)/(Q _ 2 Q _ 3) - ... + (-1)^(n - 1) (b _ 1 b _ 2 ...b _ n)/(Q _ (n - 1) Q _ n) .(13)

Two continued fractions typeset structure and typeset structure with convergents typeset structure and typeset structure, typeset structure, respectively, are called equivalent if   

B _ n/A _ n = D _ n/C _ n     for    n = 0, 1, 2, ..., ω .

Theorem ( [5] , Theorem 2.2.4): Two continued fractions typeset structure and typeset structure are equivalent if and only if  there exists a sequence of non-vanishing numbers typeset structure, typeset structure with typeset structure such that

d _ i = r _ i r _ (i - 1) b _ i , n = 1, 2, ... c _ i = r _ i a _ i , i = 0, 1, 2, ... . (14)

Consequently

Theorem: If  typeset structure, typeset structure, is an infinite sequence of non-zero complex numbers, then the continued fractions

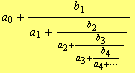a _ 0 + b _ 1/(a _ 1 + b _ 2/(a _ 2 + (   b _ 3)/(a _ 3 + b _ 4/(a _ 4 + ···) _ )))(15)

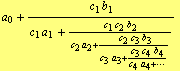a _ 0 + (c _ 1 b _ 1)/(c _ 1 a _ 1 + (c _ 1 c _ 2 b _ 2)/(c _ 2 a _ 2 + (   c _ 2 c _ 3 b _ 3)/(c _ 3 a _ 3 + (c _ 3 c _ 4 b _ 4)/(c _ 4 a _ 4 + ···))))(16)

have the same successive convergents, that is the successive convergents of continued fraction (15) are exactly the same as the convergents of the fraction (16).

Theorem ( [5]  , (2.3.19a)): Let typeset structure for every typeset structure, and

d _ 1 = b _ 1/a _ 1 , d _ i = b _ i/(a _ i a _ (i - 1))    for    n = 2, 3, ... (17)

then typeset structure and typeset structure are equivalent

If we use the formula (22) for typeset structure then we get

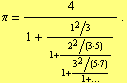π = 4/(1 + (1^2/3)/(1 + (2^2/(3 · 5))/(1 + (3^2/(5 · 7))/(1 + ...)))) .(18)

Simple continued fractions

If typeset structure for every typeset structure, then the continued fraction (1) is called simple. Simple continued fractions

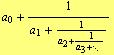a _ 0 + 1/(a _ 1 + 1/(a _ 2 + (   1)/(a _ 3 + _ ·.   )))(19)

are usually written using a more compact abbreviated notation

[a _ 0 ; a _ 1, a _ 2, a _ 3, ...] .(20)

The standard textbooks usually works only with simple continued fractions, but simple continued fractions are not necessarily “simple”. For instance, presently no regularity in the sequence of partial denominators of the simple continued fraction of π is known

π = [3 ; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13, 1, 4, 2, 6, 6, 99, 1, 2, 2, 6, 3, 5, ...](21)

On the other hand compare with a regular “non-simple” expansion

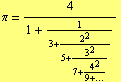π = 4/(1 + 1/(3 + 2^2/(5 + 3^2/(7 + 4^2/(9 + ...)))))(22)

which we get from (25).

Theorem: Every continued fraction (1) can be transformed into a simple continued fraction.

To see this take

c _ 1 = 1/b _ 1 , c _ 2 = b _ 1/b _ 2 , c _ 3 = b _ 2/(b _ 1 b _ 3) , ... , c _ (2 k) = (b _ 1 ... + 1)) , ...      (generally    c _ (n + 1) = 1/(c _ n b _ (n + 1)))(23)

in (16) to prove the required transformation.

Functional continued fractions

The terms of a continued fraction (1) can also be functions, say typeset structure, typeset structure, and typeset structure, typeset structure. For instance, to J.H.Lambert  [6] ,  [7]  attributed relation

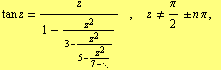tan z = z/(1 - z^2/(3 - z^2/(5 - z^2/(7 -_ ·.))))      ,       z != π/2 ± n π , (24)

appears already in L.Euler   [3]  .  Lambert used this continued fraction expansion to prove that typeset structure is irrational. He showed by an infinite descent argument that if typeset structure is rational, then the right hand side of (24) is irrational. Since typeset structure is rational, the conclusion follows (Some authors claim that Lambert's proofs is not complete. Pringsheim [8]   proved that this is not true.) Lambert gave a list of the first 27 convergents of the simple continued fraction expansion of typeset structure from which the first 25 were correct, but the last two not.

For the arc tangent we have

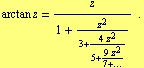arctan z = z/(1 + z^2/(3 + (4 z^2)/(5 + (9 z^2)/(7 + ...))))    .(25)

Ascending continued fractions.

Continued fractions of type (1) are called  descending continued fractions. However there are possible also other types of continued fractions. One of them are  so-called the ascending continued fractions. They were already developed by Fibonacci, Lambert or Lagrange.  

For instance, following Arabic sources Fibonacci writes (in our notation)

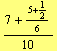(7 + (5 + 1/2)/6)/10(26)

which stands for typeset structure plus typeset structure of typeset structure plus typeset structure of typeset structure of typeset structure.

Ascending continued fractions are of the form

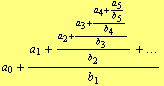a _ 0 + (a _ 1 + (a _ 2 + (a _ 3 + (a _ 4 + a _ 5/b _ 5)/b _ 4)/b _ 3)/b _ 2 + ...)/b _ 1(27)

It is equivalent with descending continued fraction

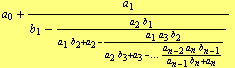a _ 0 + a _ 1/(b _ 1 - (a _ 2 b _ 1)/(a _ 1 b _ 2 + a _ 2 - (a _ 1 a _ 3 b _ 2)/(a _ 2 b _ 3 + a _ 3 - ... (a _ (n - 2) a _ n b _ (n - 1))/(a _ (n - 1) b _ n + a _ n))))(28)

References

[1]  Wallis, J. (1655). Arithmetica infinitorum .

[2]  Wallis, J. (1695). Opera mathematica I. Osord.

[3]  Euler, L. (1744). De fractionibus continuis dissertatio. Commentarii academiae scientiarum Petropolitanae, 9, 98-137 (=Opera Omnia: Series 1, Volume 14, pp. 187 - 216)   .

[4]  Perron, O. (1913). Die Lehre von den Kettenbrüchen. (German). Leipzig u. Berlin: B.G.Teubner.

[5]  Jones, W. B., & Thron, W. J. (1980). Continued fractions. Analytic theory and applications. Reading, Massachusetts, etc.: Addison-Wesley Publishing Company.

[6]  Lambert, J. H. (1761). Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques. Histoire de l'Académie Royale des Sciences et des Belles-Lettres der Berlin, 265-276.

[7]  Lambert, J. H. (1770). Vorläufige Kenntnisse für die, so die Quadratur und die Rectification des Circuls suchen.

[8]  Pringsheim, A. I. (1898). Ueber die ersten Beweise der Irrationalität von e und π. Sitzungsberichte der Bayerischen Akademie der Wissenschaften Mathematisch-Physikalische Klasse, 28, 325-337.

Cite this web-page as:

Štefan Porubský: Basic definitions for continued fractions.

Page created  .