Main Index Number Theory Arithmetic functions
Main Index Number Theory Sequences Primes
 Subject Index
comment on the page

Prime-counting function

The prime-counting function (or the prime number function) is the function counting the number of prime numbers less than or equal to some real number typeset structure. It is denoted by typeset structure and typeset structure denotes the number of primes less than or equal to typeset structure, that is

π(x) = Underoverscript[∑, p <= x, p a prime, arg3] 1 .(1)

For instance, the primes under typeset structure are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97 so typeset structure. The following table shows the highly irregular character of the graph of the prime counting function typeset structure for values typeset structure.

[Graphics:HTMLFiles/PrimeCountingFunction_12.gif]

To compute some values of the prime-counting function go to .

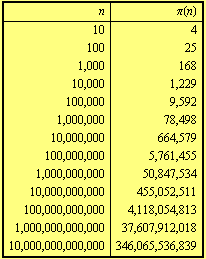
For bigger values of the argument we have the following values of the prime-counting function typeset structure.

n π(n) 10 4 100 25 1,000 ... ,000 4,118,054,813 1,000,000,000,000 37,607,912,018 10,000,000,000,000 346,065,536,839

A simple lower bound for the prime-counting function gives the following result:

Theorem.  For typeset structure we have

π(x) > log x - 1 .(2)

Proof. Consider the product

Underscript[∏, p <= x, p a prime ] (1 - 1/p)^(-1) = Underscript[∏, p <= x, p a prime ] (1 + 1/p + 1/p^2 + 1/p^3 + ...) .(3)

Every series in parentheses on the right hand is convergent, and there we can multiply then term by term. Therefore

Underscript[∏, p <= x, p a prime ] (1 - 1/p)^(-1) = ∑^' 1/n ,(4)

where the dash denotes that the sum runs over those integers typeset structure in which standard form appear only primes typeset structure. Therefore we have

∑^' 1/n >= Underoverscript[∑, n <= x, arg3] 1/n > Underoverscript[∫, 1, arg3] 1/t d t > log x .

On the other hand,

Underscript[∏, p <= x, p a prime ] (1 - 1/p)^(-1) <= Underoverscript[∏, k = ... (x) · (π(x) + 1))/(1 · 2 · 3 · ... · π(x)) = π(x) + 1.

The Theorem follows taking into account the proved inequalities.

Corollary. We have

Underscript[lim, x -> ∞] π(x) = ∞ ,(5)

that is, there are infinitely many prime numbers.

This result was for the first time proved by other means in Proposition 20 of Book IX of Euclid’s Elements.

Cite this web-page as:

Štefan Porubský: Prime-counting Function.

Page created  .