Main Index Mathematical Analysis Mathematical Constants
  Subject Index
comment on the page

Euler-Mascheroni constant

It is defined as

FormBox[RowBox[{γ, , =, RowBox[{Underscript[lim, n -> ∞]    (Underov ... 1/k - ln n), =, RowBox[{0.577, , 215, , 664, , 901, , 533, ..., Cell[]}]}]}], TraditionalForm](1)

The existence of the limit follows from the integral test for the convergence of series .

To compute typeset structure with higher precision got to  . 

We also have  integral representations

γ = Underoverscript[∫, 1, arg3] (1/⌊ x ⌋ - 1/x) d x,(2)

another one is

γ = 1 - ∫ _ 1^∞ {t}/t^2 d t .

In 1836 Dirichlet  [1]  gave the following integral  represenantion of typeset structure

γ = Underoverscript[∫, 0, arg3] (-1/(1 + t) - 1/e^t) 1/t d t .

He aslo proved that

γ = Underscript[lim, p -> 0 +] (Underoverscript[∑, n = 1, arg3] 1/n^(1 + p) - 1/p) .

The constant was first defined by Euler [2] ()   [3] . Euler denoted it by typeset structure, the notation typeset structure was introduced by Mascheroni  (1790).

The evaluation of γ is not easy. The limit defining typeset structure converges very slowly.

[Graphics:HTMLFiles/EulerMascheroni_11.gif]

Young proved that  

1/(2 (n + 1)) < Underoverscript[∑, k = 1, arg3] 1/k - ln n - γ < 1/(2 n)

and thus

Underoverscript[∑, k = 1, arg3] 1/k - ln n - γ ~ 1/(2 n) .

[Graphics:HTMLFiles/EulerMascheroni_15.gif]

Even with 4500 terms, this approximation using the definition is only good to three decimal places (despite the impression induced by the graphs above)

Underoverscript[∑, k = 1, arg3] 1/k - ln 4500 - γ = 0.000 111 107 ...

To experiment with typeset structure go to   .

Euler initially calculated the value of typeset structure to 6 decimal places. In 1736  he computed typeset structure to 15 decimal digits correctly using a more rapidly convergent expression (a special case of the so-called Euler-Maclaurin summation)

Underoverscript[∑, k = 1, arg3] 1/k - ln n - 1/(2 n) + 1/(12 n^2) - 1/(120 n^4)

Here

Underoverscript[∑, k = 1, arg3] 1/k - ln n - 1/(2 n) + 1/(12 n^2) - 1/(120 n^4) ~ -1/(252 n^6) .

More precisely, Euler used his summation formula that

1 + 1/2 + 1/3 + ... + 1/n = γ + log n + 1/(2 n) - B _ 1/(2 n^2) + B _ 2/(4 n^4) - B _ 3/(6 n^6) + ... + B _ k/(2 k n^(2 k)) + ...,(3)

where typeset structure are Bernoulli numbers (in the old odd notation) given by the generating function typeset structure.  Thus typeset structure, typeset structure, typeset structure, typeset structure. Note that the series on the right hand side is not convergent but due to fact that it is an alternating one the computation error at any stage is less than the next term in the series. Euler found that typeset structure  with typeset structure and typeset structure. Gauß later extended this by the next quadruple of digits 6060.  With typeset structure and typeset structure in  (3)  astronomer  John Couch Adams (1815-1908)     calculated typeset structure to 236 places   [4] . This required a knowledge of Bernoulli numbers  typeset structure which he previously tabulated   (Actually the first 31 Bernoulli numbers were previously computed by M.Ohm  [5]  , Adams computed 31 following ones using von Staudt theorem).

To experiment with typeset structure go to .

In 1790 Mascheroni  [6] calculated its 32 decimal places, from which only  the first 19 decimal places were correct (for more details visit   ).

In 1962 D.E.Knuth obtained 1271 digits of γ also using Euler-Maclaurin summation. The next year Sweeney  [7]  computed 3683 digits using an expansion of the exponential integral Ei(x).  Sweeney used a formula already known to Euler

Underoverscript[∑, k = 1, arg3] ((-1)^(k - 1) x^k)/(k ! k) - log x - γ = Underoverscript[∫, x, arg3] e^(-t)/t d t = O(e^(-x)/x) .

In 1980 Brent and McMillan  [8]  computed 30100 digits using identities involving modified Bessel functions in about 20 hours computer time on Univac 1100/42.  They showed that

(Underoverscript[∑, k = 0, arg3] H _ k · (x^k/k !)^n)/(Underoverscript[∑, k ... bsp;      as         x -> ∞ ,

where typeset structure is the typeset structureth harmonic number, and

c _ n = { 1 if n = 1, 2 2 n sin (π/n) if n >= 2.

They used this formula with typeset structure They also calculated the first 29200 partial quotients in the regular  continued fraction expansion for γ and proved that if  Euler-Mascheroni constant is a rational number 1 , then its denominator must be greater than typeset structure. Later Papanikolaou obtained 475006 partial quotients of its continued fraction expansion and proved that if γ is a rational number, then its denominator must exceed typeset structure. Similar results suggest that γ constant is not rational. However a proof of irrationality (let alone transcendence) seems still be beyond our possibilities. J.H. Conway and R.K. Guy  [9]   commented this by typeset structure is prepared to bet that it is transcendental.

The continued fraction representation of  γ makes it easy to find the sequence of its best rational approximations:

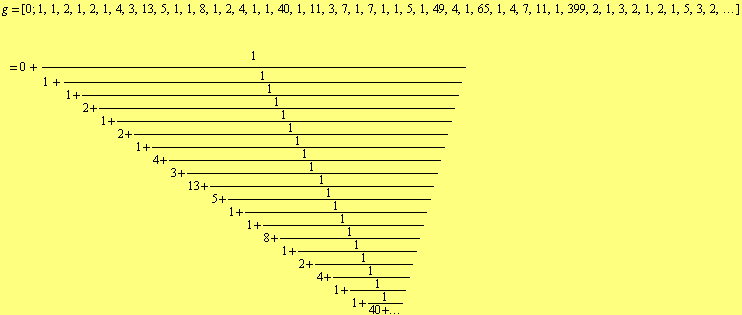
g = [0 ; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, 11, 3, 7, 1, 7, 1, 1, 5 ... 3 + 1/(5 + 1/(1 + 1/(1 + 1/(8 + 1/(1 + 1/(2 + 1/(4 + 1/(1 + 1/(1 + 1/(40 + ...)))))))))))))))))))

The first 20 convergents are

0, 1, 1/2, 3/5, 4/7, 11/19, 15/26, 71/123, 228/395, 3035/5258, 15403/26685, 18438/31943, 33841 ... /559595, 935180/1620157, 4063727/7040223, 4998907/8660380, 9062634/15700603, 367504267/636684500 .

To see the order of the approximation of a convergent go to .

A reasonable  approximation of typeset structure is given by the formula

γ ~~ 1/2 (10^(1/3) - 1) = 0. 577 21 7 345 0 ...(4)

Frederick W. Odena  [10]  gave another curious approximation

0.11111111^(1/4) = 0. 577 35(5)

D. Castellanos [11] gave these approximations

(7/83)^2/9 = 0. 577 215 209 501 1 ...,           ... sp; (990^3 - 55^3 - 79^2 - 4^2)/70^5 = 0. 577 215 664    901 5 29 ...   

In 1874 Mertens  [12]  proved that

e^γ/(ln x) ~ Underscript[∏, p <= x] (1 - 1/p) ,          as x -> ∞ ,

where the sum runs over all primes typeset structure, or in another form

Underscript[lim, n -> ∞] 1/p _ n Underoverscript[∏, k = 1, arg3] (1 - 1/p _ n)^(-1) = e^γ,(6)

where typeset structureis the typeset structureth prime. This gives an alternate expression for typeset structure

γ = Underscript[lim, x -> ∞] ( Underscript[∑, p <= x] ln p/(p - 1) - ln ln x) ,

where typeset structure runs over the all primes.

Another amusing appearance of γ in number theory shows the following result due to de la Vallée Poussin in 1898:
If a large  positive integer typeset structure is divided by each positive integer typeset structure, then the average fraction by which the quotient typeset structure falls short of the next integer is typeset structure. In other words

Underscript[lim, n -> ∞] 1/n Underoverscript[∑, k = 1, arg3] {n/k} = 1 - γ ,

Here typeset structure denotes the fractional part.

In 1838 Dirichlet proved that  

Underoverscript[∑, k = 1, arg3] d(k) = n log n + (2 γ - 1) n + O(n^(1/2))

where typeset structure denotes the divisor function counting the number of positive divisors of typeset structure.

Euler gave two zeta-function series expressions for typeset structure

γ = Underoverscript[∑, k = 2, arg3] (k - 1)/k (ζ(k) - 1) = 1 - Underoverscript[∑, k = 2, arg3] (ζ(k) - 1)/k ,(7)
γ = Underoverscript[∑, k = 2, arg3] (-1)^k ζ(k)/k,(8)

where typeset structure is the Riemann zeta function. We also have

γ = Underscript[lim, s -> 1] (ζ(s) - 1)/(s - 1) .

Since the expressions involve the Riemann zeta function they are convenient for computational purposes. Glaisher  [13]  proved a number of formulas of the type

γ = 1 - Underoverscript[∑, k = 1, arg3] ζ(2 k + 1)/((k + 1) (2 k + 1)) .

Ramanujan  [14]  proved a general formula verifying a Glaisher’s conjecture (ibid. 44, pp. 1-10)  about the existence of a general formula of the type

γ = λ _ r - Underoverscript[∑, k = 1, arg3] ((r + 1) (r + 2) ...(r + 2 k))/((2 k + 1) (2 r + 1) (2 r + 2) ...(2 r + 2 k)) ζ(2 k + 1),

for arbitrary positive integer typeset structure where typeset structure is a rational number. Ramanujan proved that

γ = Underoverscript[∫, 0, arg3] (1 + x^(2 r - 1))/(1 + x) d x - Underoverscript[&# ... g3] ((r + 1) (r + 2) ...(r + 2 k))/((2 k + 1) (2 r + 1) (2 r + 2) ...(2 r + 2 k)) ζ(2 k + 1),

for every  typeset structure. This implies that typeset structure if  typeset structure is integral.

Euler-Mascheroni constant occurs in many formulas involving Gamma function, for instance typeset structure.

The definition of typeset structure can be extended in many way. One of them says  [15]

γ = Underscript[lim, n -> ∞] [(2^m/1 + 3^m/2 + ... + n^m/(n - 1)) + m - (S _ n^0 + S _ n^1 + ... + S _ n^(m - 1)) - ln(n - 1)],

where typeset structure. If typeset structure we get the original definition.

Boas [16]  studied an analog of Euler-Mascheroni constant defined by

Underscript[lim , n -> ∞] (Underoverscript[∑, k = 1, arg3] f(k) - ∫ _ 1^n f(x) d x) .(9)

Notes

1 It is not known whether typeset structure is irrational. G. H. Hardy is said to have offered to give up his Savilian Chair at Oxford to person who proves that typeset structure is  irrational. Hilbert even said that the irrationality of typeset structure as an unsolved problem seems unapproachable.

References

[1]  Dirichlet, G. L. (1836). Sur les intégrales eulériennes. J. reine angew. Math., 15, 258-263 (Werke Vol. I, pp. 273-282, G.Reimer, Berlin 1889) .

[2]  Euler, L. (1735). De Progressionibus harmonicus observationes. Commentarii Academiæ Scientarum Imperialis Petropolitanæ , 7-1734, 150-160.

[3]  Glaisher, J. W. (1871). On the history of Euler's constant. Messenger (2), I, 25-30.

[4]  Adams, J. C. (1878). Table of the values of the first sixty-two numbers of Bernoulli. J. reine angew. Math., 85, 269-272.

[5]  Ohm, M. (1840). Etwas über die Bernoullischen Zahlen. J. reine angew. Math., 20, 11-12.

[6]  Mascheroni, L. (1790, 1792). Adnotationes ad calculum integralem Euleri, Vol. 1 and 2. . Ticino, Italy (Reprinted in Euler, L. Leonhardi Euleri Opera Omnia, Ser. 1, Vol. 12. Leipzig, Germany: Teubner, pp. 415-542, 1915.).

[7]  Sweeney, D. W. (1963, March 14). On the Computation of Euler's Constant. Math. Comput., 17(3), 170-178.

[8]  Brent, R. P., & McMillan, E. M. (1980). Some new algorithms for high-precision computation of Euler's constant. Math. Comput. , 34, 305-312.

[9]  Conway, J. H., & Guy, R. K. (1996). The Euler-Mascheroni Number. In . <Last> (Ed.), The Book of Numbers. (pp. 260-261). Berlin: Springer Verlag.

[10]  Odena, F. W. (1982/1983).. J. Recreational Math., 15(2), 118.

[11]  Castellanos, D. (1988). The ubiquitous π. Math. Mag., 61(2), 67-97.

[12]  Mertens, F. (1874). Ein Beitrag zur analytischen Zahlentheorie. Über die Verteilung der Primzahlen.. J. riene angew. Math., 78, 46-63.

[13]  Glaisher, J. W. (1914). Relations connecting quantities of the form typeset structure. Messenger, 44, 1-10.

[14]  Ramanujan, S. (1916). A series for Euler’s constant typeset structure. Messenger, 46, 73-80.

[15]  (1984, Nov.). Problem 1204. Math. Magazine, 57(5), 298  (solution  ibid. 58, No. 5. (Nov., 1985), 302 ).

[16]  Boas, R. P. (1977). Partial sums of infinite series, and how they grow. Amer. Math. Monthly, 84, 237-258.

Cite this web-page as:

Štefan Porubský: Euler-Mascheroni Constant.

Page created  and updated .