 Main Index
Main Index
 Mathematical Analysis
Mathematical Analysis
 Infinite series and products
Infinite series and products
 Infinite series
Infinite series
 Divergent series
Divergent series
 Subject Index
Subject Index
 comment on the page
comment on the page
 Main Index
Main Index
 Mathematical Analysis
Mathematical Analysis
 Infinite series and products
Infinite series and products
 Infinite series
Infinite series
 Divergent series
Divergent series
 Subject Index
Subject Index
 comment on the page
comment on the page
Let
| (1) |
If the series converges then according to the definition the sequence
| (2) |
of its partial sums is convergent, say ![]() . Then
. Then ![]() and
and ![]() . This gives the following result (for another proof visit
. This gives the following result (for another proof visit  ):
):
Theorem: If (1) is a convergent infinite series, then ![]() .
.
Or equivalently, we get
The divergence test: If (1) is an infinite series such that ![]() then the series diverges.
then the series diverges.
The following extension of the divergence test goes back to L.Olivier [1]:
Theorem: If the series (1) is convergent and its terms ![]() form a decreasing sequence
form a decreasing sequence  of positive numbers, then even
of positive numbers, then even ![]() .
.
The proof follows from Cauchy-Bolzano convergence criterion  : Given an
: Given an ![]() , there exists
, there exists ![]() such that
such that
| (3) |
for every ![]() and every
and every ![]() . Take
. Take ![]() and
and ![]() , where
, where ![]() denotes the greatest integer function. Then
denotes the greatest integer function. Then ![]() and
and ![]() . Since
. Since ![]() is decreasing, the left hand side of (3) can be estimated from below by
is decreasing, the left hand side of (3) can be estimated from below by ![]() , which implies that
, which implies that ![]() , as desired.
, as desired.
Simple example show that the assumption that ![]() is decreasing cannot be omitted ( [2] , Example 1): Define
is decreasing cannot be omitted ( [2] , Example 1): Define
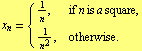
Then ![]() , but
, but ![]() , for
, for ![]() if
if ![]() is a square.
is a square.
The most natural application of this result is to show that the harmonic series  is divergent . However more can be derived using Olivier’s test: To formulate this we need the notion of the asymptotic density. If
is divergent . However more can be derived using Olivier’s test: To formulate this we need the notion of the asymptotic density. If ![]() is a subset of the set of positive integers, then the asymptotic density
is a subset of the set of positive integers, then the asymptotic density ![]() of
of ![]() is defined by
is defined by
![]()
if the limit on the right-hand side exists. We also have ( [3] , Theorem 11.1) : If ![]() exists then
exists then
![]()
The next result shows the relation between convergence of subseries of the harmonic series and the asymptotic density (for more details consult [4] and [5] ):
If ![]() is convergent then
is convergent then ![]() .
.
Note that the above theorem stems from [1] , p.34, where Olivier writes:
Donc si l’on trouve, que dans une série infinie, le produit du ![]() terms, ou du
terms, ou du ![]() des groupes de termes qui conservent le même signe, par
des groupes de termes qui conservent le même signe, par ![]() est zéro, pour
est zéro, pour ![]() , on peut regarder cette seule circonstance comme une marque, que la série est convergente, si le produit
, on peut regarder cette seule circonstance comme une marque, que la série est convergente, si le produit ![]() n’est pas nul pour
n’est pas nul pour ![]() .
.
This is an English translation according to [6] :
Therefore if one finds an infinite series, the product of the ![]() th term, or of the
th term, or of the ![]() th group of terms which keep the same sign, by
th group of terms which keep the same sign, by ![]() , is zero, for
, is zero, for ![]() , one can regard precisely this situation as an indicator that the series is convergent, and conversely, the series is not convergent if the product
, one can regard precisely this situation as an indicator that the series is convergent, and conversely, the series is not convergent if the product ![]() is nonzero for
is nonzero for ![]() .
.
That this result in this formulation is not correct was immediately pointed out by N.Abel [7] .
| [1] | Olivier, L. (1827). Remarques sur les series infinies et leur convergence. J. reine angew. Math., 2(31), 44. |
| [2] | Šalát, T., & Toma, V. (2003). A classical Olivier's theorem and statistical convergence.. Ann. Math. Blaise Pascal , 10(2), 305-313. |
| [3] | Niven, I., & Zuckerman, H. S. (1972). An introduction to the theory of numbers (3rd ed.) . New York etc.: John Wiley & Sons. |
| [4] | Šalát, T. (1964). On subseries. Math. Zeitschrift, 85, 209-225. |
| [5] | Powell, B. J., & Šalát, T. (1991). Convergence of subseries of the harmonic series and asymptotic densities of sets of positive integers . Publicationes de l’institut mathématique (Beograd) (N.S.), 50(64), 60-70. |
| [6] | Goar, M. (1999). Olivier and Abel on series convergence: An episode from early 19th century analysis. Math. Magazine, 72(5), 347-355. |
| [7] | Abel, N. (1928). Note sur le momoire de Mr. L.Olivier No.4 du second tome de ce journal, ayant pout tire ‘Remarques sur les series infinies et leur convergence'. J. reine angew. Math., 3, 79-81. |
Cite this web-page as:
Štefan Porubský: Convergence of means.