Main Index Algebraic structures Ring theory Basic notions
  Subject Index
comment on the page

Ring homomorphisms

A ring-homomorphism between rings and is a mapping such that is a monoid-homomorphism for the multiplicative structures on and , and simultaneously also a monoid-homomorphism for their additive structures. In other words, satisfies

for all , where , and denote the identity and zero element of , and , respectively.

Any ring-homomorphism which is one-to-one is called an isomorphism.

If is an ideal of the ring , and the corresponding factor ring (also called a residue class ring), then the canonical map

is a surjective ring-homomorphism, called the natural quotient map or the canonical homomorphism..

Theorem: Let be a ring-homomorphism. Then the image of is a subring of .

An injective (one-to-one) ring-homomorphism establishes a ring-isomorphism between and its image. Such a homomorphism is called an embedding (of a ring into ).

The kernel of a ring-homomorphism is an ideal of .

Theorem: If is a ring-homomorphism whose kernel contains , and is the canonical homomorphism, then there exists a unique ring-homomorphism making the following diagram commutative

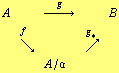
The last theorem can be equivalently rephrased saying that the canonical map is universal in the category of homomorphisms whose kernel contains the ideal .

Cite this web-page as: