 Main Index
Main Index
 Algebraic structures
Algebraic structures
 Polynomial rings
Polynomial rings
 Multivariate polynomials
Multivariate polynomials
 Identities
Identities
 Subject Index
Subject Index
 comment on the page
comment on the page
 Main Index
Main Index
 Algebraic structures
Algebraic structures
 Polynomial rings
Polynomial rings
 Multivariate polynomials
Multivariate polynomials
 Identities
Identities
 Subject Index
Subject Index
 comment on the page
comment on the page
The eight-square identity is a polynomial identity of the following form
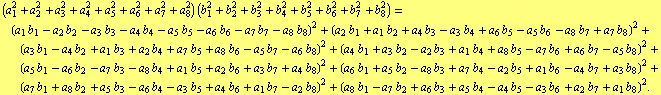 | (1) |
It can be written in many forms, for instance
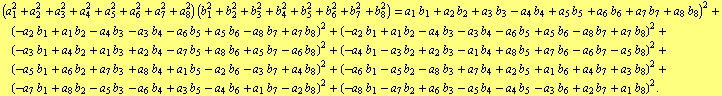 | (2) |
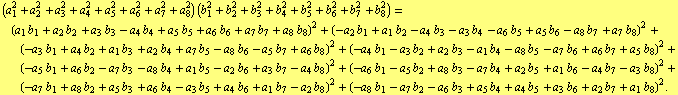 | (3) |
This type of identities were independently discovered many times. It seems that the first was the Danish mathematician C. P. Degen (1766-1825) who discovered [1] identities (2) and (3) around 1818. Degen erroneously claimed that the identity can be extended to ![]() squares. His paper went unnoticed. 1
squares. His paper went unnoticed. 1
In 1845 the mathematician Arthur Cayley (1821-1895) derived an identity of this form from the fact that the norm of the product of two octonions (or the so-called Cayley numbers) is the product of their norms [2] , [3] . Actually, the multiplication of norms of two octonions reduces to the identity
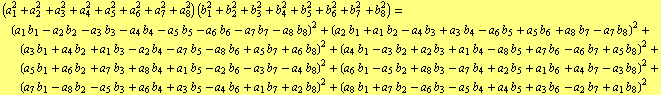 | (4) |
Prior to Cayley in 1843 they were rediscovered also by the jurist and mathematician John Thomas Graves (1806-1870) a friend of the Irish mathematician W.R. Hamilton. In October 1843 Hamilton wrote Graves about his discovery of quaternions  . In December Graves discovered octaves, however the result was published on Graves request by Hamilton only in July 1847. Graves found two variants of eight-square identity, the identity (4) and that which differs from (4) only in the interchange of indices 7 and 8 ( [2] , p. 164).
. In December Graves discovered octaves, however the result was published on Graves request by Hamilton only in July 1847. Graves found two variants of eight-square identity, the identity (4) and that which differs from (4) only in the interchange of indices 7 and 8 ( [2] , p. 164).
The eight-square identity is therefore also called the Degen-Graves-Cayley identity.
Le Besgue ( [4] , p. 65) attributes the following identity to M.Brioschi
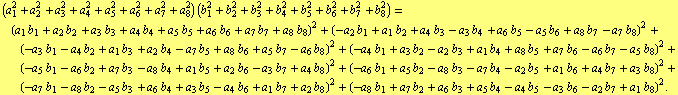 | (5) |
In 1989 Adolf Hurwitz proved that identities of this form are possible if and only if the sums of squares have 2, 4, or 8 summands  .
.
| 1 | Note, that it was Degen to whom 19 years old Niels Abel (1802-1829) submitted a “solution” to the general quintic algebraic equation. When Degen asked for a numerical example, Abel discovered a mistake in his solution, what caused to change his mind about the solvability of the general quintic in radicals, and to prove the correct opposite statement. |
| [1] | Degen, C. P. (1817-18 (1922)). Adumbratio demonstrationis theorematis arithmeticae maxime generalis. Mémoires de l'Académie Impériale des Sciences de St. Pétersbourg, 8, 207-219. |
| [2] | Dickson, L. E. (1919). On quaternions and their generalization and the history of the eight square theorem. Annals of Math., (2) 20, 155-171, 297. |
| [3] | van der Waerden, B. L. (1976). Hamilton's Discovery of Quaternions. Mathematics Magazine, 49(5), 227-234. |
| [4] | Le Besgue, V. A. (1862). Introduction a la théorie des nombres. Paris: Mallet-Bachelier. |
Cite this web-page as:
Štefan Porubský: Eight-square identity.