Vážená norma

Vnitřní potenciál RBF jednotky počítáme jako $\frac{\parallel \vec{x} - \vec{c} \parallel_{}}{b}$, kde $\parallel\vec{x}-\vec{c}\parallel$ je vzdálenost $\vec{x}$ od $\vec{c}$ počítaná dle euklidovské metriky.

Další možností je využití vážené normy, která je definována jako

$$\parallel\vec{x}\parallel ^{2}_{C} = ({\bf C}\vec{x})^T({\bf C}\vec{x}) = \vec{x}^T{\bf C}^T{\bf C}\vec{x},$$ (2.6)

kde ${\bf C}$ je matice $n\times n$ a $n$ je dimenze vstupního vektoru.

Pokud je matice ${\bf C}$ rovna jednotkové matici, dostaneme standardní euklidovskou normu.

$$\parallel\vec{x}\parallel ^{2}_{C} = \parallel\vec{x}\parallel ^2$$ (2.7)

Použití diagonální matice odpovídá přiřazení váhových koeficientů jednotlivým vstupům.

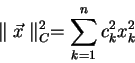$$\parallel\vec{x}\parallel ^{2}_{C} = \sum_{k=1}^{n}c_{k}^2x_{k}^2$$ (2.8)

Obecná matice představuje libovolnou afinní transformaci.

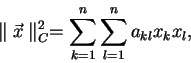$$\parallel\vec{x}\parallel ^{2}_{C} = \sum_{k=1}^{n}\sum_{l=1}^{n} a_{kl}x_k x_l ,$$ (2.9)

kde $a_{kl}$ je $kl$-tý prvek matice ${\bf C}^T{\bf C}.$

Matici ${\bf C}^T{\bf C}$ budeme dále označovat jako ${\bf\Sigma^{-1}}$. (Toto označení vychází z analogie s kovarianční maticí vícerozměrného normálního rozdělení. Pro naše účely však není tato analogie důležitá.)

Nahradíme-li euklidovskou metriku právě popsanou váženou normou, RBF síť bude počítat funkci

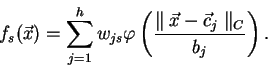$$f_s(\vec{x}) = \sum_{j=1}^{h} w_{js}\varphi\left(\frac{\parallel \vec{x} - \vec{c}_{j} \parallel_{C}}{b_j}\right).$$ (2.10)

V tomto případě všechny RBF jednotky používají při výpočtu vzdálenosti stejnou matici $C$, tedy u všech je prováděna stejná transformace.

V obecném případě může každé jednotce přidat další parametr $C$ a funkce sítě pak má tvar

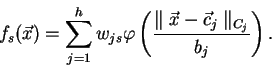$$f_s(\vec{x}) = \sum_{j=1}^{h} w_{js}\varphi\left(\frac{\parallel \vec{x} - \vec{c}_{j} \parallel_{C_j}}{b_j}\right).$$ (2.11)

Použití vážené normy je vhodné zvláště v případě, že jednotlivé složky vstupního vektoru jsou různého charakteru.