UFO

UFO is an interactive system for universal functional optimization that serves for solving both dense medium-size and sparse large-scale optimization problems. The UFO system can be used for the following applications:

• Formulation and solution of particular optimization problems.
• Preparation of specialized optimization routines (or subroutines).
• Designing and testing new optimization methods. The UFO system is a very useful tool for optimization algorithms development.

The UFO system is an open software system for solving a broad class of optimization problems. An optimization problem solution is processed in four phases. In the first phase the optimization problem is specified and an optimization method is selected. This can be made in three different ways:

• Full dialogue mode. The problem specification and the method selection are realized by using a conversation between the user and the UFO system.
• Batch mode. The problem specification and the method selection are realized by using the UFO control language. An input file written in the UFO control language has to be prepared.
• Combined mode. Only a part of the specification is written in the input file. The rest of the specification is obtained as in the dialogue mode. This possibility is usually the best one since the problem functions can be defined beforehand by using a convenient text editor.

The second phase is realized by using the UFO preprocessor. This preprocessor is written in the Fortran 77 language and its output is a Fortran 77 control program. In the third phase, the control program is translated by using a Fortran 77 compiler and a final program is linked by using library modules. In the fourth phase, the final program is executed and thus results which can be viewed by using extensive output means are obtained. A detailed description of the UFO system is contained in research report V1289-24.pdf.

The UFO system can be used for solving various dense or sparse optimization problems:

• Unconstrained or box constrained optimization.
• Optimization with general linear constraints.
• Optimization with general nonlinear constraints.
• Nonsmooth optimization.
• Global optimization.
• Solution to systems of nonlinear functional equations.
• Solution to systems of ordinary differential equations.

Moreover, the objective function can assume various forms:

• General objective function.
• Linear or quadratic objective function.
• Sum of squares (or powers) criterion.
• Minimax criterion.
• Integral criterion containing solution to ordinary differential equations.

The UFO system contains optimization methods that can be divided into the following classes:

• Heuristic methods for small-size problems. This class contains the pattern search method and the simplex method of Nelder and Mead.
• Conjugate gradient methods for large-scale problems.
• Variable metric methods which use an approximation of the Hessian matrix updated in each iteration.
• Variable metric methods with limited memory for large-scale problems.
• Variable metric methods for large-scale sparse and partially separable problems.
• Modified Newton methods which use the Hessian matrix computed either analytically or numerically.
• Modified Newton methods for large-scale sparse and partially separable problems.
• Truncated Newton methods for large-scale problems based on difference approximations of directional derivatives.
• Modified Gauss-Newton methods for nonlinear least squares which use the Jacobian matrix or the normal equation matrix.
• Modified Gauss-Newton methods for large-scale partially separable nonlinear least squares.
• Quasi-Newton methods for nonlinear least squares and nonlinear equations which use an approximation of the Jacobian matrix updated in each iteration.
• Quasi-Newton methods with limited memory for large-scale nonlinear least squares and nonlinear equations.
• Quasi-Newton methods for large-scale partially separable nonlinear least squares and nonlinear equations.
• Simplex type methods for linear programming problems.
• Interior point methods for linear programming problems.
• Simplex type methods for quadratic programming problems.
• Interior point methods for quadratic programming problems.
• Proximal bundle methods for nonsmooth optimization.
• Bundle-Newton methods for nonsmooth optimization.
• Variable metric bundle methods for nonsmooth optimization.
• Recursive quadratic programming methods for dense minimax problems.
• Recursive quadratic programming methods for dense nonlinear programming problems.
• Recursive quadratic programming methods for sparse equality constrained problems.
• Interior point methods for sparse minimax problems.
• Interior point methods for sparse nonlinear programming problems.
• Nonsmooth equation methods for sparse nonlinear programming problems.
• Random search methods for global optimization.
• Continuation methods for global optimization. This class contains tunneling function methods and filled function methods.
• Clustering methods for global optimization. This class contains a density clustering method and a single linkage clustering method.
• Multi-level methods for global optimization. Thiss class contains a multi-level single linkage clustering method and a multi-level mode analysis method.

These methods can be realized in various forms depending on the stepsize selection:

• Line search methods.
• General trust region methods.
• Special trust region methods for nonlinear least squares problems.
• Modified Marquardt methods for nonlinear least squares problems.
• SQP filter methods for nonlinear programing problems.

Moreover, various preconditioned iterative methods can be chosen for the direction determination.

The UFO system contains useful input and output possibilities:

• The UFO control language for batch inputs.
• Text dialogue for UNIX workstations.
• Graphic dialogue for PC computers.
• Basic and extended screen output.
• Graphic screen output for PC computers.
• Text file output.

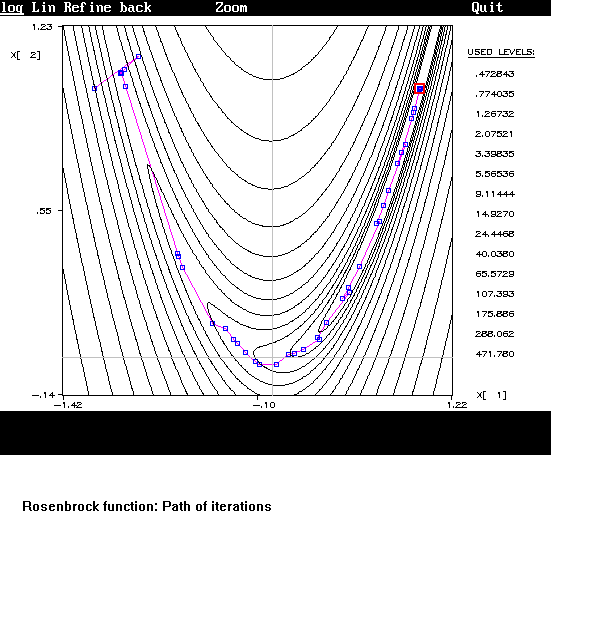
The following figure shows an example of graphic screen output: