Main Index Number Theory Sequences Recurrent sequences Linear recurrent sequences Binary recurrent sequences Lucas’ sequences Fibonacci Numbers
Subject Index
comment on the page

Cassini’s Identity

This one of the oldest identities involving Fibonacci numbers is due to the French astronomer Jean-Dominique Cassini (1625-1712) who proved it in  1680 [1] ¹:

Theorem.   for every .

1st proof.

Using relation (2) we get
.   

2nd proof.

Using the rule for formation of Fibonacci numbers we get

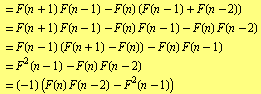The proof can be now finished using mathematical induction.      QED

Substituting   for we get this form of  Cassini’s identity

Corollary. We have

This form says that the difference between two successive ratios of Fibonacci numbers is alternatively plus or minus. Furthermore it shows that this difference gets progressively smaller confirming that the ratio does converge to a limit.

Corollary (Gelin-Cesàro identity). .

Proof. From Cassini identity we get

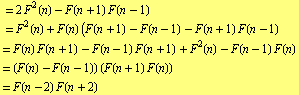Multiplying both sides by we get

If we square the Cassini identity we get

and the proof is finished.    QED

R.S.Melham [2] proved the following identity (he even presents this identity  for general second-order recurrences)

Carroll’s puzzle [3]

Cut a chess-board on the left into four pieces as shown, and the reassemble them into a rectangle on the right hand side. The original consists of squares. On the right hand side there have been rearranged to get squares. Cassini’s identity shows that when we dissect any square into four pieces with dimensions . the resulting rectangle gains or loses one square depending on whether is even or odd.

The real situation after decomposition depending on the parity of can be graphically depicted as follows:

Notes

References

Cite this web-page as: