Main Index Number Theory Arithmetics Numeral systems Non-positional numeral systems
 Subject Index
comment on the page

Roman numerals

Before the 5th century BC the Greek alphabet was divided into two principal branches, the eastern  Ionic and the wetsern Chalcidian. The differences between them were small.  After the Athens adopted the Ionic version in 403 BC, the Ionic alphabet replaced all other versions including the Chalcidian. The Chalcidian as one the alphabets used in the Greek colonies in Italy (Magna Graecia) gave probably rise to the Etruscan aphabet in the 8th century BC and thus indirectly to the other Italic alphabets.

The Etruscan numerals used by the ancient Etruscans were developed from the Greek Attic numerals ↑ . Etruscans had symbols for 1, 5, 10, 50 and 100.  One was represented by a vertical stroke I, 5 by an upside down V, 10 by a symbol similar to an X, 50 by an arrow like symbol, 100 by X with a vertical line going through its center or by a C-shaped symbol , etc. (http://users.tpg.com.au/etr/etrusk/tex/grammar.html  or   http://www.mysteriousetruscans.com/language.html#nos ).

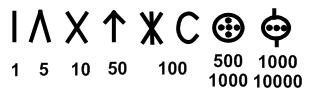
The structure of the basic Etruscan and Roman numerals system shows a quinary (or bi-quinary or quinary-decimal) character. Some theories say that the sign for 5 ensued as a half of of the sign for 10,  the sign of 50 as a half of 100.   

The Latin alphabet and the numerals were derived approximately in the 600 BC, as it was mentioned above,  from the Etruscan ones. Etruscan alphabet of 26 letters (http://users.tpg.com.au/etr/etrusk/alph/etrFont.html) was reduced to 23. The letters J, U, and W as we known them in the modern alphabet were added in medieval times, and did not appear in the classical Roman alphabet, except that J and U could be alternative forms for I and V (cf. http://www.wam.umd.edu/~rfradkin/latin.html or http://www.ancientscripts.com/latin.html ). Note that the classical Roman Latin alphabet only used capitals (i.e. the upper case or majuscule letters).

By some theories  when the Latin’s dropped the Greek letters Φ, Χ (chi) and Θ as phonetic signs, retained them as numerals, with arbitrary values. C as the symbol for one hundred developed from the Greek  Θ , or according to some other theories from a circle with a horizontal stroke or circlle with a cross, because C was the initial of the word centum. The old Φ used for 1000, or according to the mentioned theories, a circle with a vertical stroke, a thing similar ot the Greek Phi, assimilated to M. In some styles of Roman numerals the numeral D is represented by an I followed by a backwards C (ancient Roman apostrophus) ,  and M is shown as a C followed by an I and a backwards C. The number depicted  in the following picture is 1583:

Thus (I)=1000,  I)=500, and  by doubling up the outer strokes of M and the right stroke of D multiplies by 10 they got symbols like ((I))=10000, I))=5000, etc.

According to some other authors archaic form of the Roman numerals was

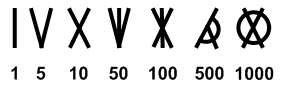
http://www.members.optusnet.com.au/ncrick/converters/romantest.html

Roman numerals as we know them are formed by  a basic set of seven literal symbols:

In Latin one is unus, five is quinque, ten is decem, fifty is quinquaginta, hundred is centum, fine hundred is quingenti and thousand is mille.  

http://www.land.salzburg.at/hs-kuchl/hsk-math/roemer1.html

To express other values the letters are placed in decreasing order of value, for example, DCLVI=666. Letters can be repeated one or two times to increase value, for example, XX = 20 and CCC = 300. With the exception of I the letters cannot be repeated more than three times, so XXXX is not used for 40, but it is acceptable to write IIII for 4. To shorten the notation the so called subtractive principle was inveted . Its general form says: The numerals are added unless there is a larger numeral anywhere to the right of a smaller one, in which case the value of the smaller numeral is subtracted from the larger numeral to its right (a subtrahend as the smaller of two numerals is preceding a greater minuend). Thus XL=40, or IV=4. The use of the subtractive principle has always been optional and its systematic use is fairly modern  (these rules only became official in the Middle Ages). On the other hand there were some regulations in its application

The above rules lead, however, not to the most economic way of writing the number values. For instance 1990 should be written as  MCMXC and not MXM, and 1999=MCMXCIX and not IMM or MIM.

http://www.tacomacc.edu/home/jkellerm/MATH106/EthnomathematicsText/Chapter2/RomanNumerals.htm

An obvious limitation of the Roman numeral system it is that it does not permit the representation of large numbers.  In the Middle Ages a horizontal line (a vinculum called a titulus in the Middle Ages)  above a particular numeral was used to to represent one thousand times that numeral (that the value is increased a thousandfold). Thus , , , etc. Additional vertical lines on both sides of the numeral (an upper half-frame) was used to to denote one 1000000 times the number Thus stoond for .

Another medieval convention said that when the second of the above rules for writing numbers was not met in front of an M (or C) then the number to the left of M (or C) denoted the number of thousands (or hundreds) which should be added to the total value located to the right of M (or C). For example, LLM denotes  .

http://www.roman-britain.org/numerals.htm

The convention about vinculum caused some problems for following the Greek custom the straight vinculum was also used simply to distinguish numerals from regular letters. Therefore little downward-pointing corner marks were added to such a multiplying vinculum. Howvere if those marks were too large, the corner marks could be misread as the above mentioned upper half-frame, which indicated multiplication by 100000. That this really happened is documented by Suetonius. Livia Drusilla (http://www.roman-emperors.org/livia.htm)  the widow of Emperor Augustus rewarded future Emperor Galba generously with either 500 000 or 50 000 000 sesterces whereas her son, the reigning Emperor Tiberius, was the residual heir. Tiberius, however, ignored her instructions and Galba never received the money. The historian Suetonius reports that quia notata non praescripta erat summa (because the intended sum had not been written out in words).

http://en.wikipedia.org/wiki/Roman_arithmetic

Basic arithmetic operations

All arithmetic operations can be broken down to combinations of addition and subtraction for multiplication is nothing else as an automated form of addition where one quickly (by heart) adds identical numbers and in division one quickly removes identical numbers. The “real” problem with Roman notation when performing arithmetic operations is the subtractive principle in notation. Consequently the most natural approach in performing the operations is to remove the subtractive notation in the first step when necessary.  

Addition:

We have two possibilities how to eliminate the the subtractive notation

The final algorithm then has the form (CDLXXVI+CCIV=?):

Subtraction:

In subtraction as a reverse operation of addition the basic idea is to cancel out the numerals of the subtrahend from the minuend (MCDLXIX-DCCCXVII=?):

Multiplication:

To multiply two numbers given in Roman numerals

It is quite a complicated task to add two Roman numerals together or even to subtract one from another, and multiplication and division are both extremely difficult. Mental arithmetic using the Roman numeric system would be beyond the capabilities of most mortal men. The dreary toil of the Roman accountant is reflected in the Latin name for the occupation, Tabularius 'the worker of tables'. The tabularius was a highly skilled - and thus highly valued - member of any senators household, though usually of the slave class, the lowest order of Roman society, he would be well looked-after for his services. The Roman accountant’s task would be simplified to some extent by the use of an abacus, or by utilising a complicated system of counting using both the digits and finger joints of each hand.

The word, "bureaucracy" stems from the word "bureau", used from the early 18th century in Western Europe not just to refer to a writing desk, but to an office, i.e. a workplace, where officials worked. The original French meaning of the word bureau was the baize used to cover desks. The term bureaucracy came into use shortly before the French Revolution of 1789, and from there rapidly spread to other countries. The Greek suffix -kratia or kratos - means "power" or "rule". Bureaucracy thus basically means office power or office rule, the rule of the officialdom.

The Romans developed their hand-abacus as a portable counting board-- the first portable calculating device for both engineers and businessmen.

In Latin calculus means "pebble." It is the diminutive of calx, meaning a piece of limestone. The counters of a Roman abacus were originally made of stone and called calculi.

http://staff.science.nus.edu.sg/~phywjs/GEM/GEMlec4.ppt#31

common remark is that multiplication and division using Roman numerals is so awkward as to be totally impractical. However, an article by James G. Kennedy in The American Mathematical Monthly in 1980 gives algorithms for these operations that are actually more straightforward in the Roman system than in the Arabic. In multiplication the first step is to rewrite the numbers in a simple place-value notation. Seven columns are set up, headed by the symbols M, D, C, L, X, V, and I, and tallies are marked in each column corresponding to the number of times that symbol appears in the multicand. For example, if the multiplicand is XIII (13), one tally is marked in the X column and three tallies are marked in the I column. The multiplier is written in the same way. The multiplication itself is done by forming partial products according to two simple rules. In most cases the partial product given by any one tally in the multiplier is simply the set of tallies that represents the multiplicand, shifted to the left an appropriate number of columns. If the multiplier digit is I, the multiplicand is not shifted at all; the multiplicand is shifted one place to the left for V, two places for X, three places for L, and so on. The second rule is applied only when one Etruscan character is multiplied by another. In such cases the tallies representing the multiplicand digit are written twice in the appropriately shifted column and an additional tally is written one column to the right. Once a partial product has been formed for every tally in the multiplier, the tallies in each column are accumulated and replaced by the Roman symbol at the head of the column, giving the final answer. Only a slight change in the method is needed for Roman numerals in "subtractive notation," where 10 is written as IX, and so on. If all this sounds not quite so simple, the method for multiplying Arabic numbers is just as involved if they are written in explicit form. Furthermore, Arabic operations require a multiplication table giving the 100 products of all the possible pairs of Arabic digits. No comparable table is needed with Roman numerals, where all arithmetical operations can be defined in terms of shifting rules, addition, and subtraction.

For examples how the Romans multiplied the numbers visit the site  http://mathforum.org/dr.math/faq/faq.roman.html#calc

It is of interest to ask what is the number of letter usedin in the Roman numeral representation of for . The first values of this sequence known as  Sloane’s A006968   are  1, 2, 3, 2, 1, 2, 3, 4, 2, 1, 2, 3, 4, ...  

Certainly, "finger calculus" systems were widespread, and capable of representing numbers up to 10,000;[12] they are still in use today in parts of the Middle East. The practice of substituting letters for numbers and vice versa, known as gematria, was also common, and it is possible that the two practices were combined to produce a finger calculus alphabet. The earliest known manual alphabet, described by the Benedictine monk Bede in 8th century Northumbria, did just that.[13] While the usual purpose of the Latin and Greek finger alphabets described by Bede is unknown, they were unlikely to have been used by deaf people for communication -- even though Bede lost his own hearing later in life. Historian Lois Bragg concludes that these alphabets were "only a bookish game [14].
[13] Bede. (710 AD). De Computo vel Loguela per Gestum Digitorum ("Of counting or speaking with the fingers"), preface to De temporum ratione ("On the reckoning of time"). Illustrated in 1140 AD, National Library, Madrid.
[14] Bragg, Lois (1997). Visual-Kinetic Communication in Europe Before 1600: A Survey of Sign Lexicons and Finger Alphabets Prior to the Rise of Deaf Education. Journal of Deaf Studies and Deaf Education 2:1 Winter 1997

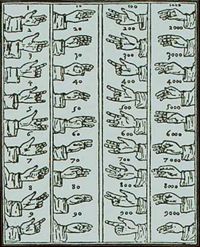
1140 AD illustration of a finger alphabet and counting system described by Bede in 710 AD. The Greek alphabet is represented, with three additional letters making a total of 27, by the first three columns of numbers. The first two columns are produced on the left hand, and the next two columns on the right

Finger Numbers in the Greco-Roman World and the Early Middle Ages
Burma P. Williams, Richard S. Williams
Isis, Vol. 86, No. 4 (Dec., 1995), pp. 587-608

http://links.jstor.org/sici?sici=0021-1753%28199512%2986%3A4%3C587%3AFNITGW%3E2.0.CO%3B2-A&size=LARGE

Arithmetical Computations in Roman Numerals
W. French Anderson
Classical Philology, Vol. 51, No. 3 (Jul., 1956), pp. 145-150

Cite this web-page as: