Main Index Number Theory Arithmetics Multiplication Divisibility
 Subject Index
comment on the page

Prime power dividing a factorial

In 1808 Legendre [1] , p. 10,     (   ) showed that

Theorem.  The exact power typeset structure of a prime typeset structure dividing typeset structure, typeset structure, is

e _ p(n !) = ⌊ n/p ⌋ + ⌊ n/p^2 ⌋ + ⌊ n/p^3 ⌋ + ... = Underscript[∑, i] ⌊ n/p^i ⌋(1)

where typeset structure denotes the integer part function    and the sum is finite containing typeset structure terms, where typeset structure is the largest power of typeset structure dividing typeset structure, i.e. typeset structure but typeset structure.

The proof is simple.  We can suppose that typeset structure. The value typeset structure counts the number of multiples of typeset structure less or equal to typeset structure. Thus there are   typeset structure positive integers typeset structure with typeset structure being the exact power of typeset structure dividing each. So the power of typeset structure dividing typeset structure equals

Underoverscript[∑, i = 1, arg3] i ( ⌊ n/p^i ⌋ - ⌊ n/p^(i + 1) ⌋ ) = Underoverscript[∑, i = 1, arg3] ⌊ n/p^i ⌋ .

Corollary 1 (Legendre). Let typeset structure be a prime and typeset structure is the base-typeset structure expansion of typeset structure.  Then

e _ p(n !) = (n - Underoverscript[∑, i = 1, arg3] a _ i)/(p - 1) .(2)

Proof. If typeset structure, then typeset structure, typeset structure, and the result holds. Let typeset structure. If  typeset structure, then    

⌊ n/p^i ⌋ = a _ i + a _ (i + 1) p + ... + a _ r p^(r - i) .

Then

3 ... + r

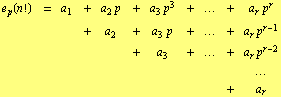
Adding columnwise we get

= a _ 1 (p - 1)/(p - 1) + a _ 2 (p^2 - 1)/(p - 1) + a _ 3 (p^3 - 1)/(p - 1) + ... + a _ r (p^r ... (a _ 0 + a _ 1 p + a _ 2 p^2 + ... + a _ r p^r) - (a _ 0 + a _ 1 + a _ 2 + ... + a _ r))/(p - 1) .

Corollary 2 (Čebyšev identity).  If typeset structure then

Underscript[∑, n <= x] ln n = ln ⌊ x ⌋ != Underscript[∑, p <= x] ln p ( ⌊ n/p ⌋ + ⌊ n/p^2 ⌋ + ⌊ n/p^3 ⌋ + ...),(3)

Corollary 3. The series typeset structure diverges (p runs over all primes).

Proof. There follows from  (2)  that  typeset structure and consequently

n ! < Underscript[∏, p <= n] p^n/(p - 1)

or that

n !^(1/n) < Underscript[∏, p <= n] p^1/(p - 1) .

Then

ln n !^(1/n) < Underscript[∑, p <= n] (ln p)/(p - 1) <= 2 Underscript[∑, p] (ln p)/p .

Since typeset structure, the result follows.

Corollary 4. If  typeset structure denotes the sums of digits function in base typeset structure then

e _ p(((2 n)/n)) = (2 s _ p(2 n) - s _ p(n))/(p - 1) .

References

[1]  Legendre, A. M. (1808). Essai sur la theorie des nombres (2ed.). Paris.

Cite this web-page as:

Štefan Porubský: Prime power dividing a factorial.

Page created  .