Main Index Mathematical Analysis Special Functions
  Subject Index
comment on the page

Signum Function

The signum function is the real valued function defined for real typeset structure as follows

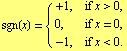
sgn(x) = {+ 1, if x > 0, 0, if x = 0, -1, if x < 0.

[Graphics:HTMLFiles/SignumFunction_3.gif]

For all real typeset structure we have  typeset structure. Similarly,  typeset structure. If typeset structure then also typeset structure. The second property implies that for real non-zero typeset structure we have typeset structure.  

For a complex argument typeset structure it is defined by

sgn(z) = { 0, if z = 0, z -----, | z | if z != 0,

where typeset structure denotes the magnitude (absolute value) of typeset structure. In other words, the signum function project a non-zero complex number to the unit circle typeset structure.

We have typeset structure, where typeset structure is the complex conjugate of typeset structure.

Cite this web-page as:

Štefan Porubský: Signum Function.

Page created  .