Main Index Mathematical Analysis Mathematical Constants
  Subject Index
comment on the page

Theorem: is irrational.

The square root of  2 was probably the first known irrational number. The first know proof of its irrationality is attributed to the Pythagorean Hippasus of Metapontum (500 B.C.).  His proof  is not known, maybe it was geometrical as the following one:

Proof 1: Suppose that is a rational number, say with coprime, i.e. is written in its lowest term.. Then , or . By Pythagorean theorem there is a right isosceles triangle with hypotenuse of length and legs .  Let be such a triangle.

Let and . Since  , the triangles and are congruent by SAS. This implies that is half a right angle, and consequently is also a right isosceles triangle. Since , also . The triangles and are similar right isosceles triangles (). Moreover , and they are congruent, and therefore . Hence we constructed a right isosceles triangle with hypotenuse of length and legs . Since the similarity of triangles preserves the ratio of corresponding sides of triangles, we have . On the other hand   (for ) and (due to the triangle inequality). A contradiction with the hypothesis that is in lowest terms.

The above proof can be put in an arithmetic form as follows:

Proof 2: Assume that   can be written as a fraction with in lowest terms. Then both are positive and since we also have . Consider the identity

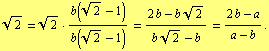
Since   and the so-called method of infinite descent finishes the proof.

The French mathematician Michel Mendès-France and Mike Keane found independently the following modification of the above proof:

Proof 3: We know that and suppose that is rational. Let , , be minimal such that . Then and . But is also a positive integer, a contradiction.  

Note that this idea is applicable to prove the irrationality of the square root of any integer which is not a perfect square because then such a root falls between two consecutive integers.

The most common proofs of the irrationality of employs some form of the unique factorization theorem. The simplest one depends on the subdivision of integers into even and odd ones.

Proof 4:  Suppose that with coprime. Then , and consequently, must be even, say . Substituting back we get ,a nd similarly   is even too. But evenness of both and contradict the assumption that are coprime.  

This proof can again be generalized to show that any root of any natural number is either a natural number or irrational

An alternative use of  the unique factorization theorem is as follows:

Proof 5:  Suppose that with coprime, then . By the unique factorization theorem, both and have a unique prime factorization, which yields that and , where are non-negative odd integers, and   are nonnegative integers. Inserting back we get the equality . But this contradicts the uniqueness of the prime factorizations having two distinct factorizations , one with an even power of 2, and other with an odd power of 2.

The Babylonian clay tablet YBC 7289 (c. 1800-1600 BCE)    gives an approximation of  in four sexagesimal figures:

The Babylonians used for its approximation method now called “Babylonian method” and which is a special case of what we now called Newton’s method. It can be used for approximation of any with desired accuracy. It proceeds as follows:

1) start with an approximation . The closer to the root, the better,

2) then use the arithmetic mean to approximate the geometric mean:

In Indian mathematics from the Vedic period   we know the Shulba Sutras which are part of the larger corpus of texts called the Shrauta Sutras. These are texts belonging to the Srauta ritual and contain geometry related to fire-altar constructions. Altar construction surprisingly also led to an estimation of the square root of 2. In the Baudhayana sutra we can find :

2.12. The measure is to be increased by its third and this [third] again by its own fourth less the thirty-fourth part [of that fourth]; this is [the value of] the diagonal of a square [whose side is the measure].

This gives:

The square root of two has the following continued fraction representation:

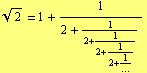
Its first 15  convergents are

Cite this web-page as:

Štefan Porubský:  .