 Main Index
Main Index
 Mathematical Analysis
Mathematical Analysis
 Mathematical Constants
Mathematical Constants
 Subject Index
Subject Index
 comment on the page
comment on the page
 Main Index
Main Index
 Mathematical Analysis
Mathematical Analysis
 Mathematical Constants
Mathematical Constants
 Subject Index
Subject Index
 comment on the page
comment on the page
The number ![]() is called the golden ratio. It is also known as the golden mean, the golden section and divine proportion or ratio (this name appears for the first time in the 1500's and was used till the 19th century. Martin Ohm (1792-1872), a younger brother of physicist Georg Ohm, is believed to be the first to use the term golden ratio
is called the golden ratio. It is also known as the golden mean, the golden section and divine proportion or ratio (this name appears for the first time in the 1500's and was used till the 19th century. Martin Ohm (1792-1872), a younger brother of physicist Georg Ohm, is believed to be the first to use the term golden ratio  ).
).
To compute the golden ration with higher precision go to  .
.
Thus the Golden ratio is an algebraic number of order 2. Its minimal polynomial is ![]() (see below). The second root of this polynomial is
(see below). The second root of this polynomial is ![]()
Note that the reciprocal ![]() called golden ratio conjugate (or also silver ratio) has minimal polynomial
called golden ratio conjugate (or also silver ratio) has minimal polynomial ![]() . The first known approximate decimal expansion of the (inverse) golden ratio as "about 0.6180340" was given in 1597 by M.Maestlin (1550-1631) in a letter to J.Kepler (1571-1630).
. The first known approximate decimal expansion of the (inverse) golden ratio as "about 0.6180340" was given in 1597 by M.Maestlin (1550-1631) in a letter to J.Kepler (1571-1630).
The ancient Greeks believed that the proportion ![]() is the most pleasing, and therefore all of their sculpture 1, architecture elements, etc. made use of this proportion. A rectangle whose sides had this proportion was called the Golden Rectangle.
is the most pleasing, and therefore all of their sculpture 1, architecture elements, etc. made use of this proportion. A rectangle whose sides had this proportion was called the Golden Rectangle.
Plato in his Timaeus, considered the golden section to be the most binding of all mathematical relationships and the key to the physics of the cosmos.
In Definition 3 of Book VI of Euclid’s Elements we can read: A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.
![[Graphics:HTMLFiles/GoldenRatio_7.gif]](HTMLFiles/GoldenRatio_7.gif)
In terms of an equation we get
| (1) |
If we set the length ![]() to be
to be ![]() and
and ![]() to represent the length of
to represent the length of ![]() , then
, then
| (2) |
This also gives the equation ![]() , or
, or ![]() , that is
, that is ![]() for
for ![]() .
.
Euclid in Proposition 30 of Book VI of his Elements referred to dividing a line at the point 0.6180399... as dividing a line in the extreme and mean ratio. A construction how to cut a line segment in this manner appears earlier in Proposition 11 of Book II in an equivalent form stated in terms of rectangles: To cut a given straight line so that the rectangle contained by the whole and one of the segments equals the square on the remaining segment. The construction is then used in Book IV in order to construct regular pentagons and 15-sided polygons (Propositions 10 through 12 and 16). Another substantial part of Elements related to pentagon is in Book XIII. The important information for determination of the diagonal of pentagon is contained in Proposition 8 of Book XIII: If in an equilateral and equiangular pentagon straight lines subtend two angles are taken in order, then they cut one another in extreme and mean ratio, and their greater segments equal the side of the pentagon.
![[Graphics:HTMLFiles/GoldenRatio_21.gif]](HTMLFiles/GoldenRatio_21.gif)
The blue triangle left has its sides in the golden ratio with its base, and the red triangle in the middle has its base in the golden ratio with one of the sides. The last fact can used to construct a regular pentagon
![[Graphics:HTMLFiles/GoldenRatio_25.gif]](HTMLFiles/GoldenRatio_25.gif)
To divide a given line segment ![]() into extreme and mean ratio follow the following procedure:
into extreme and mean ratio follow the following procedure:
![[Graphics:HTMLFiles/GoldenRatio_47.gif]](HTMLFiles/GoldenRatio_47.gif)
The numerical value of the golden ratio ![]() to
to ![]() decimal places can be obtained by command:
decimal places can be obtained by command:
If
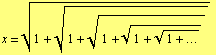
then ![]() , that is
, that is

Along similar lines we can prove the continued fraction expansion
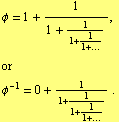
Ramanujan gave the following continued fraction expansion involving the golden ratio
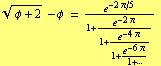
| 1 | For instance the Greek sculptor and mathematician Phidias (500 BC - 432 BC) applied it to the design of sculptures for the Parthenon. |
Cite this web-page as:
Štefan Porubský: Golden Ratio.