Main Index Mathematical Analysis Infinite series and products Infinite series Series with arbitrary terms
  Subject Index
comment on the page

Alternating series

These are infinite series of the form

with for every , that is the terms of the series alternate in sign.

Alternating Series Test (Leibniz):  If the alternating series satisfies

(i)    for , and

(ii)

then the series is convergent.

The proof follows runs along similar ideas as the proof of the convergence alternating harmonic series    with the difference that now applies the same reasoning to the expression

This test only tells when a series converges and not if a series will diverge. The test can be extended in such a way that it is required that eventually we will have for all after some point.  Thus it is possible for the first few terms of a series do not decrease.  

Example: Let . If , then

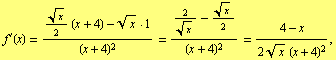
which is negative for , and so is decreasing for , which implies that the series satisfies the alternating series test when its first three terms are omitted.

Simple examples show that condition (i) cannot be omitted.

Take a divergent positive term series whose terms go to zero, say , and a convergent series with positive terms, say .  Then interfuse the first with the second one to form the following series

(1)

This is an alternating series which terms go to zero, but the terms do not form a monotone decreasing sequence. The resulting series diverges since the divergent harmonic series overpowers the contribution of the convergent series to force the th partial sum off to .

Graph of the absolute values of terms of series  (1). Red points represent the terms of series  , blue ones the terms of .

The Alternating Series Error Estimate: Suppose that is a sequence of real numbers which satisfies the hypothesis of the alternating series test. Suppose that the series converges to . Let . Then .

A series with positive terms can be converted to an alternating series using the transformation

where .

To find the explicit values for alternating series is a more complicated question. For instance,

(2)

Graph of the absolute values of terms of series  (2). Blue points represent the absolute value of negative terms.

The series on the left hand side of  (2) is sometimes called the alternating harmonic series.

Euler discovered the following formula for :

(3)

We also have

(4)

(5)

B. Schmuland  [1]   studied properties of the random harmonic series

(6)

where the , , are independent random variables taking the values   and with common distribution . He noticed that Kolmogorov’s three series theorem  or martingale convergence theorem imply that the sequence of th partial sums of (6) converges almost surely. He proved that the sum (6) has a uniform distribution on and describes some interesting properties of the convergent as random variable.

References

Cite this web-page as: