Main Index Mathematical analysis Infinite series and products Infinite products
  Subject Index
comment on the page

Infinite products

Infinite product appeared for the first time [1]  in the work of Viète [2] , p. 400, who found the product involving

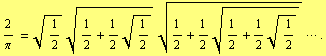
Almost simultaneously in 1656 J.Wallis [3] , p. 468, found the expression

Euler later found many infinite product expressions, but the rigorous convergence theory of infinite products was initiated by Cauchy.

An infinite product is an expression of the form

This infinite product is called convergent

• if there exists such that for all ,
• the sequence of partial products converges to a non-vanishing limit, say .

Otherwise the product is said to diverge. If both conditions are satisfied the product is assigned the value . Because of the first condition it is often used the notation indicating that it is sufficient to consider the products only from some index onwards. For the sake of simplicity, in what follows we shall always start with .

There follows from the definition that a convergent infinite product vanishes if and only if on of its factors vanishes.

Theorem: If an infinite product converges then  ..

Previous result motivates to denote the factors of an infinite product in the form , where if the product is convergent we can suppose that , that is to consider the products of the type

(1)

Theorem (Cauchy-Bolzano criterion): The infinite product converges if and only if  for every there exists such that for every   and every   we have

Theorem: The infinite product converges if and only if the series converges for some (here we take the principal branch of the logarithm).

Proof. Without loss of generality we can suppose that . Let , and be the th partial sum of the infinite series and the th product of the infinite product, respectively. Then .

Suppose that the series converges and let . Then by continuity

and the Theorem is proved in one direction.

In the opposite direction the problem is caused by the fact that does not converge to but to one of its branches.

For every there is an integer such that

Taking the difference we get

and thus for the arguments we have

Since , l as . Thus the first two terms on the right hand side are approaching each other, while the absolute values of the last term is at most . Consequently, for all sufficiently large , and the series converges.

Absolutely convergent infinite products

An infinite product is called absolutely convergent if the product is convergent.

Theorem: The product converges absolutely if and only if the series converges absolutely.

Theorem: If the product converges then also the product converges.

Theorem: The product converges absolutely if  the series converges and the series converges absolutely.

Note that if and if converges then clearly it converges absolutely, but this is not true for complex .

Theorem: If the series converges absolutely and if for we have , then

exists and is finite and non-vanishing.

Note that  the previous result does not depend on the convergence behavior of the series .

To the proof note that  , that is

Since the ’s are bounded, the exponent in the second factor converges, and the Theorem follows.

Corollary: If the series converges absolutely, the series and the product have the same convergence behavior.

Infinite products with non-negative terms

If in  (1) the numbers are non-negative, the product is called with non-negative terms.

Theorem: The product with converges if and only if the series converges.

Theorem: The product with converges if and only if the series converges.

The products and are convergent for and divergent for .  

If then monotonically decreases and consequently converges. If in addition diverges the , and the product   diverges to 0.

References

Cite this web-page as: