Main Index Algebraic structures Ring theory Special rings
  Subject Index
comment on the page

Factor ring

Ideals are important because they appear as kernels of ring homomorphisms and allow one to define factor rings.

Given a ring   and a two-sided ideal , define the following equivalence relation ~ on :  

(1)

The equivalence is a congruence relation. If , then~ we say that and are congruent modulo . The equivalence class of the element is given by

(2)

This equivalence class is also written as or simply and it called the residue class of modulo .

The set of all such equivalence classes is denoted by , and it  becomes a ring, the so-called the factor ring or quotient ring or residue class ring of R modulo I, if we define its operation as follows

(3)

(4)

These definitions are well-defined and  the corresponding structure on is a ring. The ring is a ring with (multiplicative) identity, namely . The zero-element of is .

The map is a surjective ring homomorphism, called the natural quotient map or the canonical homomorphism.

The natural quotient map provides a bijection between the two-sided ideals of R that contain a and the two-sided ideals of .

Theorem. There exists a one-to-one correspondence (bijection) preserving the inclusion between the ideals that contain and ideals of the factor ring .

The same assertion is also true for left and for right ideals containing .

The natural quotient map has the so-called universal property in the category of homomorphisms whose kernel contains the ideal . This means:

Theorem. Let be a ring homomorphism. Its kernel is an ideal of  . If the kernel contains the ideal , then there exists precisely one ring homomorphism such that , where is the natural quotient map.

The map is given by the rule for all .

Previous theorem can be also formulated in the following way:

Theorem: If is a ring-homomorphism whose kernel contains , and is the natural quotient map, then there exists a unique ring-homomorphism making the following diagram commutative

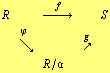
Cite this web-page as: