 Main Index
Main Index
 Algebraic structures
Algebraic structures
 Polynomial rings
Polynomial rings
 Univariate polynomials
Univariate polynomials
 Subject Index
Subject Index
 comment on the page
comment on the page
 Main Index
Main Index
 Algebraic structures
Algebraic structures
 Polynomial rings
Polynomial rings
 Univariate polynomials
Univariate polynomials
 Subject Index
Subject Index
 comment on the page
comment on the page
The classical algorithm for dividing one polynomial by another one is based on the so-called long division algorithm which basis is formed by the following result.
Division algorithm for polynomials: Let ![]() be a field. If
be a field. If ![]() and
and ![]() are polynomials in
are polynomials in ![]() , with
, with ![]() 1, there exist unique polynomials
1, there exist unique polynomials ![]() and
and ![]() such that
such that ![]() and
and ![]() .
.
It is customary to call ![]() (polynomial) quotient and
(polynomial) quotient and ![]() the (polynomial) remainder.
the (polynomial) remainder.
We shall prove this result because the given proof is constructive and provides a hint how to realize the long division.
Let
![]()
![]()
If ![]() the result is obvious because it is sufficient to take
the result is obvious because it is sufficient to take ![]() and
and ![]() . So let us assume that
. So let us assume that ![]() . Since
. Since ![]() is a field, every non-zero element has its multiplicative inverse in
is a field, every non-zero element has its multiplicative inverse in ![]() , especially there exists
, especially there exists ![]() . Consider the polynomials
. Consider the polynomials
Obviously, ![]() . If
. If ![]() the procedure ends. Suppose therefore that
the procedure ends. Suppose therefore that ![]() . If we denote by
. If we denote by ![]() the leading coefficient of polynomial
the leading coefficient of polynomial ![]() and by
and by ![]() its degree, then let
its degree, then let
Again, ![]() . If
. If ![]() the procedure ends. If
the procedure ends. If ![]() , then we proceed analogically as in the previous step to find polynomial
, then we proceed analogically as in the previous step to find polynomial ![]() . Since the degrees of polynomials
. Since the degrees of polynomials ![]() with growing index
with growing index ![]() decrease, after a finite number of steps we reach a value less than
decrease, after a finite number of steps we reach a value less than ![]() . Let
. Let ![]() denote the number of these steps, i.e.
denote the number of these steps, i.e.
while ![]() . Put
. Put
![]()
Then the backwards substitution yields that
![]()
and the first conclusion of the Theorem about the existence follows.
Finally, in order to establish the uniqueness of ![]() and
and ![]() , let us suppose that
, let us suppose that ![]() has two representations of the required form
has two representations of the required form
![]()
with ![]() and
and ![]() . Then
. Then
![]()
Since ![]() , this equality can hold only if
, this equality can hold only if ![]() , i.e.
, i.e. ![]() and
and ![]() .
.
Example: The long division of polynomials demonstrated in the previous proof can be practically realized as follows:
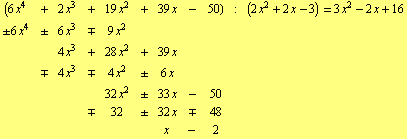
i.e. ![]() .
.
The assumption that ![]() is a field is essential, it is not possible to replace it, for instance, by a weaker assumption that
is a field is essential, it is not possible to replace it, for instance, by a weaker assumption that ![]() is a ring, because the division process by the leading coefficient of polynomial
is a ring, because the division process by the leading coefficient of polynomial ![]() could possibly not have been carried out in
could possibly not have been carried out in ![]() if
if ![]() is “only” a ring. Clearly, the division can be realized if the leading coefficient of
is “only” a ring. Clearly, the division can be realized if the leading coefficient of ![]() has its multiplicative inverse in
has its multiplicative inverse in ![]() , for instance, when the leading coefficient is
, for instance, when the leading coefficient is ![]() or
or ![]() .
.
| 1 |
Cite this web-page as:
Štefan Porubský: Division of Polynomials.