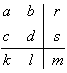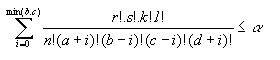GUHA - basic information
1. GUHA (General Unary
Hypotheses Automaton) is a method of automatic generation of
hypotheses based on empirical data, thus a method of data mining.
GUHA is one of the oldest methods of data mining
(the first papers appeared in mid-sixties) and still develops. It
is a kind of automated exploratory data analysis: it generates
systematically hypotheses supported by the data.
2. GUHA is primary suitable for
exploratory analysis of large data.
The processed data form a rectangle matrix, where rows
corresponds to objects belonging to the sample and each column
correspond to one investigated variable. A typical data matrix
processed by GUHA has hundreds or thousands of rows and tens of
columns.
Exploratory analysis means that there is no single specific
hypothesis that should be tested by our data; rather, our aim is
to get orientation in the domain of investigation, analyze the
behaviour of chosen variables, interactions among them etc. Such
inquiry is not blind but directed by some general (possibly vague)
direction of research (some general problem).
3. GUHA systematicaly creates
all hypotheses interesting from the point of view of a given
general problem and on the base of given data.
This is the main principle: "all interesting hypotheses''
Clearly, this contains a dilemma: "all'' means most possible,
"only interesting'' means "not too many''. To cope with
this dilemma, one may use different GUHA procedures and, having
selected one, by fixing in various ways its numerous parameters.
(The program leads the user and makes the selection of parameters
easy.)
Three remarks:
- GUHA procedures polyfactorial hypotheses i.e. not only
hypotheses relating one variable with another one, but
expressing relations among single variables, pairs,
triples, quadruples of variables etc.
- GUHA offers hypotheses. Exploratory character implies
that the hypotheses produced by the computer (numerous in
number: typically tens or hundreds of hypotheses) are
just supported by the data, not verified. You are assumed
to use this offer as inspiration, and possibly select
some few hypotheses for further testing.
- GUHA is not suitable for testing a single hypothesis:
routine packages are good for this.
4. The GUHA procedure ASSOC
generates statements on association between complex boolean
attributes (properties). These attributes are constructed from
the variables corresponding to the columns of the data matrix.
Each such variable endowed with a (finite) set of categories,
each category being by a subset of the range of the variable. A literal
has the form VAR:CAT where VAR is a variable and CAT one of
its categories (e.g. TEMPERATURE:(>38) etc.) A hypothesis (or
better: an observational statement) has the form  (
( is
associated with
is
associated with 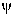 ) where attributes
) where attributes 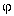 ,
,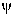 are built from literals
using boolean connectives
are built from literals
using boolean connectives 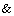 ,
, 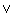 ,
,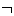 (conjunction, disjunction, negation)
Typically only some boolean attributes are allowed, e.g. only
conjunctions of finitely many literals, containing each variable
at most once, e.g.
(conjunction, disjunction, negation)
Typically only some boolean attributes are allowed, e.g. only
conjunctions of finitely many literals, containing each variable
at most once, e.g.
TEMPERATURE:(>38) & PRESURE:HIGH &
SEX:MALE
5. Given the data,
each pair of boolean attributes 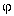 ,
,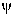 determines its four-fold
frequency table; the association of
determines its four-fold
frequency table; the association of 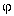 with
with 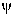 is defined by choosing
an associational quantifier
is defined by choosing
an associational quantifier 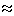 i.e. a function assigning to each four-fold
table either 1 (associated) or 0 (not associated) and satisfying
some natural monotonicity conditions. The formula
i.e. a function assigning to each four-fold
table either 1 (associated) or 0 (not associated) and satisfying
some natural monotonicity conditions. The formula 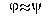 is
true in the data iff the function defining
is
true in the data iff the function defining 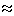 gives 1 to the four-fold
table (a,b,c,d) given
by
gives 1 to the four-fold
table (a,b,c,d) given
by 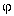 ,
, 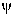
The four-fold table has the form:
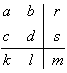
where a=Fr(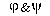 ) -- the number of
objects in the data satisfying both
) -- the number of
objects in the data satisfying both 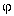 and
and 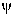 ; b=Fr(
; b=Fr(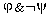 )
(satisfying
)
(satisfying 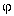 but not satisfying
but not satisfying 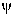 ), similarly
), similarly
c=Fr(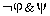 ), d=Fr(
), d=Fr(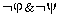 );
r, s, k, l are marginals, i.e.
r=a+b, r=c+d, b=a+c, l=b+d and in is
the cardinality of the set of objects (the number of rows of the
data matrix, m=a+b+c+d).
);
r, s, k, l are marginals, i.e.
r=a+b, r=c+d, b=a+c, l=b+d and in is
the cardinality of the set of objects (the number of rows of the
data matrix, m=a+b+c+d).
Association means, roughly, that there are enough coincidences (a,
d are big enough) and not too many differences (b, c
are not too big).
Thus a quantifier q(a, b, c,
d) is associational if q(a, b,
c, d)=1 and a' 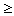 a, b'
a, b'
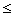 b,
c'
b,
c' 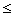 c, d'
c, d' 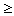 d imply q(a',
b', c', d')=1.
d imply q(a',
b', c', d')=1.
6. There are various types of
associational quantifiers, formalizing various kind of
associations; among them implicational
quantifiers formalize the association
"many 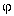 are
are 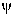 ''. Comparative quantifiers
formalize the association "
''. Comparative quantifiers
formalize the association "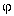 makes
makes 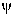 more
likely (than
more
likely (than 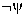 does).'' Some quantifiers just express observations
on the data, some others serve as tests of statistical hypotheses
on unknown probabilities.
does).'' Some quantifiers just express observations
on the data, some others serve as tests of statistical hypotheses
on unknown probabilities.
We give you examples:
founded p-implication: FIMPLp,B(a,
b, c, d)=1 iff a 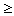 B and
a/(a+b)
B and
a/(a+b) 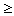 p
p
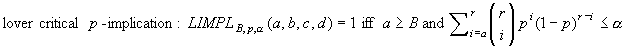
(test of 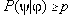 with significance alpha)
with significance alpha)
Comparative:
simple comparison: SIMPLE(a, b, c,
d)=1 iff ad > bc
Fisher test: 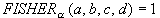 iff ad > bc and
iff ad > bc and
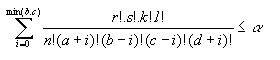
(test of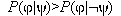 with significance alpha)
with significance alpha)
All quantifiers are associational; the implicational ones do
not depend on c, d the comparative ones are
symmetric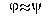 implies
implies 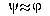 and admit negation
and admit negation 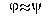 implies
implies 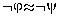 ).
Various other quantifiers are used.
).
Various other quantifiers are used.
Remark: The association rules as defined in various
papers dealing with data mining are closely related to formula 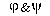 where
where
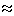 is
FIMPL.
is
FIMPL.
7. The input for the GUHA
procedure ASSOC (like for other possible GUHA procedures)
consists of (1) the data matrix and (2) parameters determining
symbolic restriction to the pairs 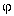 ,
,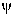 of boolean attributes (antecedent
-- succedent) to be generated, the quantifier to be used and a
few other things.
of boolean attributes (antecedent
-- succedent) to be generated, the quantifier to be used and a
few other things.
In particular, one has to declare variables that can occur in the
antecedent and the succedent, minimal and maximal length of
antecedent/succedent (number of literals occurring), the kind and
parameters of the quantifier used, kind of processing of missing
data (if any; three possibilities) etc.
8. The core program produces all
associations 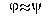 satisfying the syntactic restrictions and true in the
data.
satisfying the syntactic restrictions and true in the
data.
The generation is not done blindly but uses various techniques
serving to avoid exhaustive search. The found associations
together with various parameters are not mechanically printed but
saved in a solution file for further processing.
9. The program for
interpretation of results enables the user to browse the
associations format, sort them according to various criteria,
select reasonably defined subsets and output concise information
of various kinds.
10. There is a running PC-implementation under DOS (PC-GUHA), some few years old
and now becoming old-fashioned; the full program and manual are
freely available. Besides, we are developing a new implementation
GUHA+- under Windows; a beta version exists and is (was)
demonstrated at PKDD'99.
The new implementation is a work of a group of students of the
Faculty of Mathematics and physics, Charles University (who
worked under the guidance of Dr. A. Sochorova and is being
further developed at the institute of Computer Science of the
Academy of Sciences of the Czech Republic. We mention in passing
another implementation developed at the Prague University of
Economics under the name 4FT-Miner.
11. The method has sufficiently
deep logical and statistical foundations, continuously developed
further
The oldest paper in english is [1]; it contains already
the FIMPL quantifier and explicit formulation of the basic
principle. The monograph [4] which is the basic theoretical
reference, presents generated logical systems both for
observational statements (on data) and for probabilistic
statements, theorems on their logical properties, principles of
statistical inference, various techniques for handling missing
information etc. For selected publications concerning theory and
implementation see [1-14] other publications see the bibliography.
12. There have been several
application described in the literature; but still the method has
remained rather unknown. It is hoped that the data mining
community will soon recognize GUHA as one of the oldest data
mining methods and will enrich its foundations by the theory of
GUHA -- like systems.
For selected recent papers referring on applications of GUHA see
[15 - 20]
References:
[1] Hájek P., Havel, Chytil M.:
The GUHA method of automatic hypotheses determination, Computing
1 (1966) 293--308.
[2] Hávranek T.: The statistical
modification and interpretation of GUHA method, Kybernetika 7
(1971) 13--21.
[3] Hájek P., Bendová K., Renc Z.:
The GUHA method and three-valued logic, Kybernetika 7 (1971)
421--431.
- processing missing information
[4] Hájek P., Havránek T.:
Mechanizing Hypothesis Formation (Mathematical Foundations for a
General Theory, Springer--Verlag 1978, 396 pp.
[5] Hájek P., Havránek T.: The
GUHA method - its aims and techniques, Int. J. Man-Machine
Studies 10 (1977) 3-22.
[6] Hájek P., Havránek T., Chytil M.:
Metoda GUHA (in Czech), Academia Prague, 1983, 314 pp.
[7] Hájek P.: The new version of
the GUHA procedure ASSOC, COMPSTAT 1984, 360--365.
[8] Hájek P., Sochorová A., Zvárová
J.: GUHA for personal computers, Comp. Stat., Data
Arch. 19, 149--153.
[9] Holeňa M.: Exploratory data
processing using a fuzzy generalization of the GUHA approach. In Fuzzy
Logic, J. Baldwin, Ed. John Wiley and Sons, New York, 1996,
pp. 213--229.
[10] Rauch J.: Logical Calculi
for Knowledge Discovery in Databases, Principles of Data Mining
and Knowledge Discovery. Red. Komorowski, J. Zytkow, J. Berlin, Springer
Verlag 1997, p. 47 - 57.
[11] Hájek P., Holena M.: Formal
logics of discovery and hypothesis formation by machine. In Discovery
Science. Red. Arikava, S. and Motoda, eds.), Springer Verlag 1998,
Berlin, pp. 291-302.
[12] Rauch J.: Four-Fold Table
Calculi for Discovery Science. ibid. pp.405-406
[13] Harmancová D., Holena M., and
Sochorová A.: Overview of the GUHA method for automating
knowledge discovery in statistical data sets. In Procedings
of {KESDA'98} -- International Conference on Knowledge Extraction
from Statistical Data (1998) M. Noirhomme-Fraiture, Ed., pp.
39--52.
[14] Holena M.: Fuzzy hypotheses
for GUHA implications. Fuzzy Sets and Systems 98 (1998),
101--125.
[15] Hálová J., Zák P., Strouf O.:
QSAR of Catechol Analogs Against Malignant Melanoma by PC-GUHA
and CATALYSTTMsoftware systems, poster, VIII. Congress
IUPAC, Geneve (Switzerland) 1997. Chimia 51 (1997), 532.
[16] Hálová J., Strouf O., Zák P.,
Sochorová A., Uchida N., Yuzuvi T., Sakakibava K., Hirota M.:
QSAR of Catechol Analogs Against Malignant Melanoma using
fingerprint descriptors, Quant. Struct.-Act. Relat. 17 (1998),
37--39.
[17] Kausitz J., Kulliffay P., Puterová
B., and Pecen L.: Prognostic meaning of cystolic
concentrations of ER, PS2, Cath-D, TPS, TK and cAMP in primary
breast carcinomas for patient risk estimation and therapy
selection. To appear in International Journal of Human Tumor
Markers.
[18] Pecen L., and Eben K.: Non-linear
mathematical interpretation of the oncological data. Neural
Network World, 6:683--690, 1996.
[19] Pecen L., Pelikán E., Beran H.,
and Pivka D.: Short-term fx market analysis and prediction.
In Neural Networks in Financial Engeneering (1996), pp.189-196.
[20] Pecen L., Ramesová N., Pelikán E.,
and Beran H.: Application of the GUHA method on financial
data. Neural Network World 5 (1995), 565--571.
Contact addresses:
D. Coufal, P. Hájek
Institute of Computer Science
Academy of Sciences of the Czech Republic
Pod vodarenskou vezi 2
182 07 Prague 8, Czech Republic
e-mail: <coufal,hajek>@cs.cas.cz
web: www.cs.cas.cz